Question

1．已知△ACB、△ADE为等腰直角三角形，∠ABC=∠ADE=90°，连CD、BE，M、N分别为BE、CD的中点．
（1）如图1，若点D在AB上，点E在AC上，请作出点E关于N点对称点F并直接写出线段MN与BD的数量关系MN=$\frac{1}{2}$BD、位置关系NM⊥BD；
（2）如图2，将△ADE绕点A顺时针旋转，求$\frac{MN}{BD}$的值；
（3）如图3，将△ADE绕点A顺时针旋转一个锐角，如果线段BC的中点为P，BC=2$\sqrt{5}$，CE=3$\sqrt{2}$，当PD∥CE时，请直接写出线段PD的长2$\sqrt{2}$．

Answer 1

分析 （1）如图1中，由此EN交BC于F，点F就是所求的点，只要证明△NCF≌△NDE，即可解决问题．
（2）如图2中，将△DBA绕点B逆时针旋转90°得到△BCH，则HC=AD=DE，△BDH是等腰直角三角形，DH=$\sqrt{2}$BD，只要证明四边形CHDE是平行四边形，即可解决问题．
（3）如图3中，作CN∥DE交DP的延长线于N，连接BN、BD，作BM⊥PD于M，延长AD、CN交于点G，先证明△BCN≌△BAD，推出△BDN是等腰直角三角形，再L利用勾股定理即可解决问题．

解答 解：（1）如图1中，由此EN交BC于F，点F就是所求的点．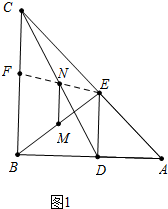

理由：∵∠ADE=∠ABC=90°，
∴DE∥BC，
∴∠FCN=∠EDN，
在△NCF和△NDE中，
$\left\{\begin{array}{l}{∠FCN=∠EDN}\\{CN=ND}\\{∠CNF=∠END}\end{array}\right.$，
∴△NCF≌△NDE，
∴NF=NE．
∴点F与点E关于点N对称．
∵AD=DE，DE=CF，
∴CF=AD，∵BC=BA，
∴BD=BF，
∵EN=NF，EM=MB，
∴MN∥AB，MN=$\frac{1}{2}$BF=$\frac{1}{2}$BD．
∵AB⊥BD，
∴MN⊥BD，
故答案为MN=$\frac{1}{2}$BD，MN⊥BD．

（2）如图2中，将△DBA绕点B逆时针旋转90°得到△BCH，则HC=AD=DE，△BDH是等腰直角三角形，DH=$\sqrt{2}$BD．

∵∠BAC=∠DAE=45°，
∴∠BAD=∠CAE，
∵$\frac{AC}{AB}$=$\frac{AE}{AD}$=$\sqrt{2}$，
∵△ACE∽△ABD，
∴EC=$\sqrt{2}$BD=HD，∵HC=DE
∴四边形CHDE是平行四边形，CD与EH互相平分，
∴点N是CD与EH的交点，
∴NE=NH，∵ME=MB，
∴BH=2MN，
∴$\frac{MN}{BD}$=$\frac{1}{2}$．

（3）如图3中，作CN∥DE交DP的延长线于N，连接BN、BD，作BM⊥PD于M，延长AD、CN交于点G．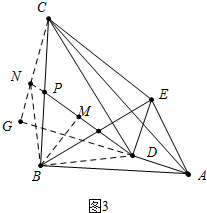

∵CN∥DE，DN∥CE，
∴四边形CNDE是平行四边形，
∴CN=DE=AD，
∵AG⊥DE，DE∥CN，
∴AG⊥CG，
∴∠CGA=∠CBA=90°，
∴∠BCN=∠BAD，
∵BC=BA，CN=AD，
∴△BCN≌△BAD，
∴BD=BN，∠NBC=∠DBA，∠NBD=∠ABC=90°，
∴∠BDM=45°，
由（2）可知BD=$\frac{\sqrt{2}}{2}$CE=3，
∴BM=MD=$\frac{3\sqrt{2}}{2}$，
在Rt△PBM中，PM=$\sqrt{P{B}^{2}-B{M}^{2}}$=$\sqrt{5-\frac{9}{2}}$=$\frac{\sqrt{2}}{2}$，
∴PD=PM+MD=$\frac{\sqrt{2}}{2}$+$\frac{3\sqrt{2}}{2}$=2$\sqrt{2}$．
故答案为2$\sqrt{2}$．

点评 本题考查几何变换综合题、全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、平行四边形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．