
已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
(1)如图,当△ABC是等边三角形时,请你写出满足图中条件,四个成立的结论;

(2)如图,当△ABC中只有∠ACB=60°时,请你证明S△ABC与S△ABD的和等于S△BCE与S△ACE的和.

解:(1)略.每正确地写出一个结论得1分,共4分.
(2)
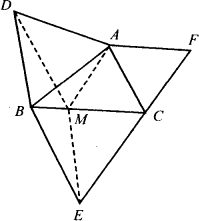
解:过A作AM∥FC交BC于M,连结DM、EM.
因为∠ACB=60°,∠CAF=60°,
所以∠ACB=∠CAF.
所以AF∥MC.
所以四边形AMCF为平行四边形.
又因为FA=FC,所以![]() AMCF为菱形.
AMCF为菱形.
所以AC=CM=AM,且∠MAC=60°.
在△BAC与△EMC中,CA=CM,∠ACB=∠MCE,CB=CE,
所以△BAC≌△EMC.
所以BA=EM.
在△ADM与△ABC中,AM=AC,∠DAM=∠BAC,DA=BA,
所以△ADM≌△ABC.
所以DM=BC.
则DM=EB,DB=EM.
所以四边形DBEM为平行四边形.
所以S△BDM+S△DAM+S△MAC=S△BEM+S△EMC+S△ACF.
即S△ABC+S△ABD=S△BCE+S△ACF.


科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com