
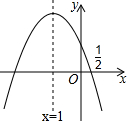 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:| A. | ①②③ | B. | ①③④ | C. | ①②③⑤ | D. | ①③⑤ |
分析 根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号及运用一些特殊点解答问题.
解答 解:解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以-$\frac{b}{2a}$=-1,可得b=2a,
a-2b+4c=a-4a+4c=-3a+4c,
∵a<0,
∴-3a>0,
∴-3a+4c>0,
即a-2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),
∴抛物线与x轴的另一个交点坐标为(-$\frac{5}{2}$,0),
当x=-$\frac{5}{2}$时,y=0,即a(-$\frac{5}{2}$)2-$\frac{5}{2}$b+c=0,
整理得:25a-10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴$\frac{1}{2}$b+b+c<0,
即3b+2c<0,故④错误;
当x=-1时,a-b+c>am2-bm+c,
∴a-b≥m(am-b),故⑤正确;
故选D.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 矩形的对角线互相垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
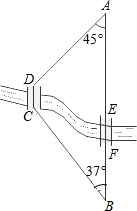 如图所示,A,B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A⇒D⇒C⇒B到达.现在新建了一座同样长的桥EF,可直接沿直线AB从A地到达B地.已知BC=10km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地可比原来少走多少路程(结果精确到0.1km.参考数据:$\sqrt{2}$≈1.41,sin37°≈0.60,cos37°≈0.80)
如图所示,A,B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A⇒D⇒C⇒B到达.现在新建了一座同样长的桥EF,可直接沿直线AB从A地到达B地.已知BC=10km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地可比原来少走多少路程(结果精确到0.1km.参考数据:$\sqrt{2}$≈1.41,sin37°≈0.60,cos37°≈0.80)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩/分 | 36 | 37 | 38 | 39 | 40 |
| 人数/人 | 1 | 2 | 1 | 4 | 2 |
| A. | 这10名同学体育成绩的中位数为38分 | |
| B. | 这10名同学体育成绩的平均数为38分 | |
| C. | 这10名同学体育成绩的众数为39分 | |
| D. | 这10名同学体育成绩的方差为2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
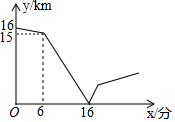 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com