
”¾ĢāÄæ”抔ŗĘøł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹż![]() µÄĶ¼ĻńŗĶŠŌÖŹ½ųŠŠÉīČėĢ½¾æ£¬¹ż³ĢČēĻĀ£¬Ēė²¹³äĶźÕū£®
µÄĶ¼ĻńŗĶŠŌÖŹ½ųŠŠÉīČėĢ½¾æ£¬¹ż³ĢČēĻĀ£¬Ēė²¹³äĶźÕū£®
×Ō±äĮæ![]() µÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬
µÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬![]() Óė
Óė![]() µÄ¼ø×é¶ŌÓ¦ŹżÖµČēĻĀ±ķ£ŗ
µÄ¼ø×é¶ŌÓ¦ŹżÖµČēĻĀ±ķ£ŗ
| ” |
|
|
|
|
| 0 | 0£®5 | 1 | 1£®5 | 2 |
| ” |
| ” |
|
|
|
|
| 0 |
|
|
|
| 0 | ” |
±ķÖŠ![]() µÄÖµŹĒ_______£®
µÄÖµŹĒ_______£®
£Ø2£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬Ćč³öĮĖŅŌÉĻ±ķÖŠ²æ·Ö¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļń£®
ÖŠ£¬Ćč³öĮĖŅŌÉĻ±ķÖŠ²æ·Ö¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļń£®
£Ø3£©Ąą±ČÅ×ĪļĻß![]() £¬ŹŌ“ÓĶ¼ĻńµÄÖį¶Ō³ĘŠŌ”¢Ōö¼õŠŌ”¢ÓŠĪŽ×īֵȿøö·½Ćę·Ö±šĖµĆ÷ŗÆŹż
£¬ŹŌ“ÓĶ¼ĻńµÄÖį¶Ō³ĘŠŌ”¢Ōö¼õŠŌ”¢ÓŠĪŽ×īֵȿøö·½Ćę·Ö±šĖµĆ÷ŗÆŹż![]() ¾ßÓŠµÄŠŌÖŹ£ŗ£Øø÷Š“Ņ»Ģõ¼“æÉ£©
¾ßÓŠµÄŠŌÖŹ£ŗ£Øø÷Š“Ņ»Ģõ¼“æÉ£©
___________________________________________________________________________
£Ø4£©½ųŅ»²½Ģ½¾æŗÆŹżĶ¼Ļń·¢ĻÖ£ŗ
¢ŁŗÆŹżĶ¼ĻńÓė![]() ÖįÓŠ_______øö½»µć£¬ĖłŅŌ¶ŌÓ¦µÄ·½³Ģ
ÖįÓŠ_______øö½»µć£¬ĖłŅŌ¶ŌÓ¦µÄ·½³Ģ![]() ÓŠ______øöŹµŹżøł£»
ÓŠ______øöŹµŹżøł£»
¢Ś·½³Ģ![]() ÓŠ_______øöŹµŹżøł£»
ÓŠ_______øöŹµŹżøł£»
¢Ū¶Ō¹ŲÓŚ![]() µÄ·½³Ģ
µÄ·½³Ģ![]() £¬Ä£·Ā¢ŚŠ“³öŅ»øöÕęĆüĢā£®
£¬Ä£·Ā¢ŚŠ“³öŅ»øöÕęĆüĢā£®
____________________________________________________________
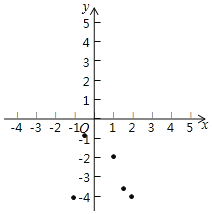
”¾“š°ø”æ£Ø1£©3£»£Ø2£©Ķ¼Ļó¼ū½āĪö£»£Ø3£©¢ŁøĆŗÆŹżµÄĶ¼Ļó²»¾ßÓŠ¶Ō³ĘŠŌ£»¢Śµ±x£¼0Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó£ØŗĻĄķ¼“æÉ£©£»¢ŪøĆŗÆŹżĆ»ÓŠ×ī“óÖµŗĶ×īŠ”Öµ£®£Ø4£©¢Ł2£¬2£»¢Ś2£»¢Ūµ±-4£¼a£¼0Ź±£¬¹ŲÓŚxµÄ·½³Ģ£¬x3-3x2=aÓŠČżøöŹµŹżøł£»
”¾½āĪö”æ
£Ø1£©µ±y=0Ź±£¬x3-3x2=0£¬x2£Øx-3£©=0£¬ĖłŅŌx=0£¬x=3
£Ø2£©ĆčµćĮ¬Ļß»³öĶ¼ŠĪ
£Ø3£©¹Ū²ģĶ¼Ļó¼“æÉ
£Ø4£©¹Ū²ģĶ¼Ļó¼“æÉ
£Ø1£©µ±y=0Ź±£¬x3-3x2=0£¬x2£Øx-3£©=0£¬ĖłŅŌx=0(ÉįČ„)£¬x=3
¹Ź“š°øĪŖ£ŗ3.
£Ø2£©Ķ¼ĻóČēĶ¼ĖłŹ¾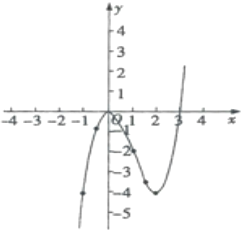
£Ø3£©¢ŁøĆŗÆŹżµÄĶ¼Ļó²»¾ßÓŠ¶Ō³ĘŠŌ£»
¢Śµ±x£¼0Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó£ØŗĻĄķ¼“æÉ£©£»
¢ŪøĆŗÆŹżĆ»ÓŠ×ī“óÖµŗĶ×īŠ”Öµ£®
£Ø4£©øł¾ŻŗÆŹżĶ¼ĻóæÉµĆ£ŗ¢Ł2£¬2
¢Ś2
¢Ū“š°ø²»ĪØŅ»£¬Čēµ±-4£¼a£¼0Ź±£¬¹ŲÓŚxµÄ·½³Ģ
x3-3x2=aÓŠČżøöŹµŹżøł


 ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
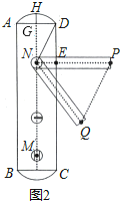
”¾ĢāÄæ”抔Ć÷¼ŅµÄĆÅæņÉĻ×°ÓŠŅ»°Ń·ĄµĮĆÅĖų£ØČēĶ¼1£©£¬ĘäĘ½Ćę½į¹¹Ķ¼ČēĶ¼2ĖłŹ¾£¬ĖųÉķæÉŅŌ擳ÉÓÉĮ½ĢõµČ»”![]() £¬
£¬![]() ŗĶ¾ŲŠĪ
ŗĶ¾ŲŠĪ![]() ×é³ÉµÄ£¬
×é³ÉµÄ£¬![]() µÄŌ²ŠÄŹĒµ¹Ėų°“Å„µć
µÄŌ²ŠÄŹĒµ¹Ėų°“Å„µć![]() £®ŅŃÖŖ
£®ŅŃÖŖ![]() µÄ¹ŠĪøß
µÄ¹ŠĪøß![]() £¬
£¬![]() £¬
£¬![]() £®µ±Ėų±ś
£®µ±Ėų±ś![]() ČĘ×ŵć
ČĘ×ŵć![]() Ė³Ź±ÕėŠż×ŖÖĮ
Ė³Ź±ÕėŠż×ŖÖĮ![]() Ī»ÖĆŹ±£¬ĆÅĖų“ņæŖ£¬“ĖŹ±Ö±Ļß
Ī»ÖĆŹ±£¬ĆÅĖų“ņæŖ£¬“ĖŹ±Ö±Ļß![]() Óė
Óė![]() ĖłŌŚµÄŌ²ĻąĒŠ£¬ĒŅ
ĖłŌŚµÄŌ²ĻąĒŠ£¬ĒŅ![]() £¬
£¬![]() £®
£®
£Ø1£©Ēó![]() ĖłŌŚŌ²µÄ°ė¾¶£»
ĖłŌŚŌ²µÄ°ė¾¶£»
£Ø2£©ĒóĻ߶Ī![]() µÄ³¤¶Č£®£Ø
µÄ³¤¶Č£®£Ø![]() £¬½į¹ū¾«Č·µ½
£¬½į¹ū¾«Č·µ½![]() £©
£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćPŹĒĻŅACÉĻŅ»¶Æµć£Ø²»ÓėA£¬CÖŲŗĻ£©£¬¹żµćP×÷PE”ĶAB£¬“¹×ćĪŖE£¬ÉäĻßEP½»![]() ÓŚµćF£¬½»¹żµćCµÄĒŠĻßÓŚµćD£®
ÓŚµćF£¬½»¹żµćCµÄĒŠĻßÓŚµćD£®

£Ø1£©ĒóÖ¤£ŗDC=DP£»
£Ø2£©Čō”ĻCAB=30”ć£¬µ±FŹĒ![]() µÄÖŠµćŹ±£¬ÅŠ¶ĻŅŌA£¬O£¬C£¬FĪŖ¶„µćµÄĖıߊĪŹĒŹ²Ć“ĢŲŹāĖıߊĪ£æĖµĆ÷ĄķÓÉ£®
µÄÖŠµćŹ±£¬ÅŠ¶ĻŅŌA£¬O£¬C£¬FĪŖ¶„µćµÄĖıߊĪŹĒŹ²Ć“ĢŲŹāĖıߊĪ£æĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻABC£½90”ć
£Ø1£©ČēĶ¼1£¬·Ö±š¹żA”¢CĮ½µć×÷¾¹żµćBµÄÖ±Ļߵē¹Ļߣ¬“¹×ć·Ö±šĪŖµćM£¬N£¬ĒóÖ¤£ŗ”÷ABM”×”÷BCN£»
£Ø2£©ČēĶ¼2£¬PŹĒBC±ßÉĻŅ»µć£¬”ĻBAP£½”ĻC£¬tan”ĻPAC£½![]() £¬BP£½2cm£¬ĒóCPµÄ³¤£®
£¬BP£½2cm£¬ĒóCPµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
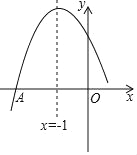
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa£¬b£¬cŹĒ³£Źż£¬a”Ł0£©Ķ¼ĻóµÄ¶Ō³ĘÖįŹĒÖ±Ļßx=©1£¬ÓėxÖįµÄŅ»øö½»µćŹĒA£Ø©3£¬0£©ĘäĶ¼ĻóµÄŅ»²æ·ÖČēĶ¼ĖłŹ¾£¬¶ŌÓŚĻĀĮŠĖµ·Ø£ŗ¢Ł2a=b£»¢Śabc£¾0£¬¢ŪČōµćB£Ø©2£¬y1£©£¬C£Ø©![]() £¬y2£©ŹĒĶ¼ĻóÉĻĮ½µć£¬Ōņy1£¼y2£»¢ÜĶ¼ĻóÓėxÖįµÄĮķŅ»øö½»µćµÄ×ų±źĪŖ£Ø1£¬0£©£®ĘäÖŠÕżČ·µÄŹĒ_____£Ø°ŃÕżČ·Ėµ·ØµÄŠņŗŶ¼ĢīÉĻ£©
£¬y2£©ŹĒĶ¼ĻóÉĻĮ½µć£¬Ōņy1£¼y2£»¢ÜĶ¼ĻóÓėxÖįµÄĮķŅ»øö½»µćµÄ×ų±źĪŖ£Ø1£¬0£©£®ĘäÖŠÕżČ·µÄŹĒ_____£Ø°ŃÕżČ·Ėµ·ØµÄŠņŗŶ¼ĢīÉĻ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°“å“åĶع«Ā·Õž²ß£¬ŹĒ½üÄźĄ“¹ś¼Ņ¹¹½ØŗĶŠ³Éē»į£¬Ö§³ÖŠĀÅ©“å½ØÉčµÄŅ»ĻīÖŲ“󹫹²¾ö²ß£¬ŹĒŅ»ĻīĆńŠÄ¹¤³Ģ£¬»ŻĆń¹¤³ĢijÕņÕžø®×¼±øĻņ¼×”¢ŅŅĮ½øö¹¤³Ģ¶Ó·¢°üŅ»¶Ī”°“å“åĶØ”±¹¤³Ģ½ØÉčĻīÄ棬¾µ÷²é£ŗ¼×”¢ŅŅĮ½¶Óµ„¶ĄĶź³ÉøĆ¹¤³Ģ£¬ŅŅ¶ÓĖłŠčŹ±¼äŹĒ¼×¶ÓµÄ2±¶£»¼×”¢ŅŅĮ½¶Ó¹²Ķ¬Ķź³ÉøĆ¹¤³ĢŠč30Ģģ£»Čō¼×¶ÓĆæĢģĖłŠčĄĶĪń·ŃÓĆĪŖ2400ŌŖ£¬ŅŅ¶ÓĆæĢģĖłŠčĄĶĪń·ŃÓĆĪŖ1500ŌŖ£¬“Ó½ŚŌ¼×Ź½šµÄ½Ē¶Čæ¼ĀĒ£¬Ó¦Ń”ŌńÄÄøö¹¤³Ģ¶ÓøüŗĻĖć£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¶ŹÆ»śŹĒ¹Å“śµÄ“óŠĶ¹„³ĒĪäĘ÷£¬ŹĒŹżŃ§”¢¹¤³Ģ”¢ĪļĄķµČø“ŌÓѧæĘĻą»„ČŚŗĻµÄÓ¦ÓĆ£ØČēĶ¼£Ø1£©£©£®ŌŚĪŅ¹ś”¶ŌŖŹ·”¤ŅąĖ¼ĀķŅņ“«”·ÖŠ¶ŌÕāÖÖĶ¶ŹÆ»ś¾ĶÓŠ¹ż¼ĒŌŲ£ØČēĶ¼£Ø2£©£©£®
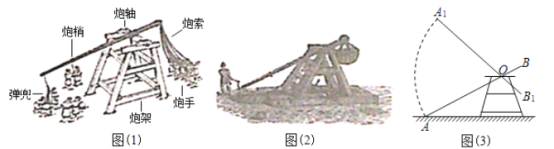
Ķ¼£Ø3£©ŹĒĶ¼£Ø1£©ÖŠČĖ¹¤Ķ¶ŹÆ»śµÄ²ąĆęŹ¾ŅāĶ¼£¬ÅŚ¼ÜµÄŗįĻņÖ§¼Ü¾łÓėµŲĆęĻą»„Ę½ŠŠ£¬ŅŃÖŖ![]() Ć×£¬ÅŚÖį¾ąµŲĆę4.5Ć×£¬
Ć×£¬ÅŚÖį¾ąµŲĆę4.5Ć×£¬![]()
![]() £¬ÅŚÉŅ¶„¶Ėµć
£¬ÅŚÉŅ¶„¶Ėµć![]() Äܵ½“ļĖ®Ę½µŲĆę£¬×īøßµćÄܵ½“ļµć
Äܵ½“ļĖ®Ę½µŲĆę£¬×īøßµćÄܵ½“ļµć![]() “¦£¬ĒŅŠż×ŖµÄ¼Š½Ē
“¦£¬ĒŅŠż×ŖµÄ¼Š½Ē![]() £Øµć
£Øµć![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ŌŚĶ¬Ņ»Ę½ĆęÄŚ£©£¬Ēóµć
ŌŚĶ¬Ņ»Ę½ĆęÄŚ£©£¬Ēóµć![]() µ½Ė®Ę½µŲĆęµÄ¾ąĄė£®£Ø²Īæ¼Źż¾Ż£ŗ
µ½Ė®Ę½µŲĆęµÄ¾ąĄė£®£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży£½x£«mµÄĶ¼ĻóÓė·“±ČĄżŗÆŹży£½![]() µÄĶ¼Ļó½»ÓŚA£¬BĮ½µć£¬ĒŅÓėxÖį½»ÓŚµćC£¬µćAµÄ×ų±źĪŖ(2£¬1)£®
µÄĶ¼Ļó½»ÓŚA£¬BĮ½µć£¬ĒŅÓėxÖį½»ÓŚµćC£¬µćAµÄ×ų±źĪŖ(2£¬1)£®
(1)Ēóm¼°kµÄÖµ£»
(2)ĒóµćCµÄ×ų±ź£¬²¢½įŗĻĶ¼Ļ󊓳ö²»µČŹ½×é0£¼x£«m”Ü![]() µÄ½ā¼Æ£®
µÄ½ā¼Æ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
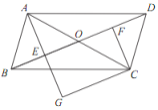
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”õABCD ÖŠ£¬¶Ō½ĒĻß AC Óė BD Ļą½»ÓŚµć O £¬µć E £¬ F ·Ö±šĪŖ OB £¬ OD µÄÖŠµć£¬ŃÓ³¤ AE ÖĮ G £¬Ź¹ EG £½AE £¬Į¬½Ó CG £®
£Ø1£©ĒóÖ¤£ŗ ”÷ABE”Õ”÷CDF £»
£Ø2£©µ± AB Óė AC Āś×ćŹ²Ć“ŹżĮæ¹ŲĻµŹ±£¬ĖıߊĪ EGCF ŹĒ¾ŲŠĪ£æĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com