
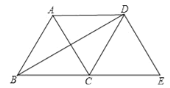
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是________________(填写正确的序号).
【答案】①②③
【解析】
根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD.
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,
∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,
∴∠ACD=120°60°=60°,
∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE,
∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴BD⊥AC,
∴①②③都正确,
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,以点 A 为圆心,AB 长为半径画弧交 AD 于点 F,再分别以点 B、F 为圆心,大于![]() BF 的相同长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点 E,连接 EF.
BF 的相同长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点 E,连接 EF.
(1)根据以上尺规作图的过程,证明四边形 ABEF 是菱形;
(2)若菱形 ABEF 的边长为 2,AE= 2 ![]() ,求菱形 ABEF 的面积.
,求菱形 ABEF 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
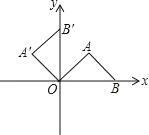
【题目】在直角坐标系中,等腰直角三角形AOB在如图所示的位置,点B的横坐标为2,将△AOB绕点O按逆时针方向旋转90°,得到△A′OB′,则点A′的坐标为( )
A. (1,1) B. (![]() ,
,![]() )
)
C. (﹣1,1) D. (﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
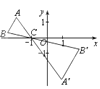
【题目】如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. -![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①,图②均是![]() 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段
的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段![]() 的端点都在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
的端点都在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
(1)在图①中画一个钝角![]() ,且点
,且点![]() 在格点上,使它有一边与该边上的高线长度相等;
在格点上,使它有一边与该边上的高线长度相等;
(2)在图②中画一个五边形![]() ,使其是轴对称图形,且
,使其是轴对称图形,且![]() ,点
,点![]() 、
、![]() 、
、![]() 在格点上.
在格点上.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com