
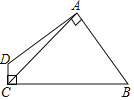
【题目】如图,四边形ABCD中,AB=AD,AC=6,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.

(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距40km,甲、乙两人沿同一路线从A地到B地,甲骑自行车先出发,1.5h后乙乘坐公共汽车出发,两人匀速行驶的路程与时间的关系如图所示.
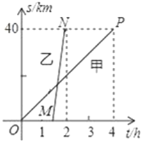
(1)求甲、乙两人的速度;
(2)若乙到达B地后,立即以原速返回A地.
①在图中画出乙返程中距离A地的路程y(km)与时间x(h)的函数图象,并求出此时y与x的函数表达式;
②求甲在离B地多远处与返程中的乙相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.
(1)求a,b的值;(2)请计算这道题的正确结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

【答案】![]()
【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点![]() ,
,
![]() ,
,
![]() 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
![]() 点P的坐标为
点P的坐标为![]() .
.
故答案为:![]() .
.
【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 分别交x轴、y轴于A、B两点(AOAB)且AO、AB的长分别是一元二次方程x23x20的两个根,点C在x轴负半轴上,且AB:AC=1:2.
分别交x轴、y轴于A、B两点(AOAB)且AO、AB的长分别是一元二次方程x23x20的两个根,点C在x轴负半轴上,且AB:AC=1:2.
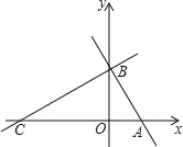
(1)求A、C两点的坐标;
(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com