【题目】如图，已知AB=AC，∠A=36°，AB的中垂线交AC于点E，交AB于点D，下面4个结论：
①射线BE是∠ABC的平分线；②△BCE是等腰三角形；③△ABE是等腰三角形；④△ADE≌△BDE；
（1）判断其中正确的结论是哪几个？
（2）从你认为是正确的结论中选一个加以说明．
【答案】(1) ①②③④;（2）证明见解析.
【解析】试题分析：(1)利用垂直平分线到两端点距离相等，证明③正确，再证明④中三角形全等，利用等腰三角形底角相等，说明∠ABE=∠CBE, ①正确,所以②△BCE是等腰三角形.①②③④均正确.(2)同（1）
试题解析：
(1) AB的中垂线交AC于点E，
AE=BE,
△ABE是等腰三角形, ③正确.
AD=AD,AE=BE,∠ADE=∠BDE,
△ADE≌△BDE,④正确.
AB=AC，∠A=36°，
∠C=72°.∠EBC=36°，
射线BE是∠ABC的平分线①正确.
∠BEC=72°.
△BCE是等腰三角形，②正确.
①②③④都正确.
(2)证明见（1）详解.
科目：初中数学 来源： 题型：
【题目】关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1、x2
（1）求实数k的取值范围。
（2）若方程两实根x1、x2满足x1+x2=﹣x1x2，求k的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A、F、C、D在同一条直线上，已知AF=DC，∠A=∠D，BC∥EF，求证：AB=DE．
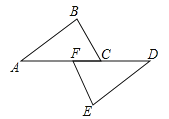
【答案】证明见解析．
【解析】试题分析：欲证明AB=DE，只要证明△ABC≌△DEF即可．
试题解析：∵AF=CD，
∴AC=DF，
∵BC∥EF，
∴∠ACB=∠DFE，
在△ABC和△DEF中，
，
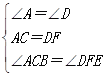∴△ABC≌△DEF（ASA），
∴AB=DE．
考点：全等三角形的判定与性质．
【题型】解答题
【结束】
25
【题目】如图， 
，AE=BD，点D在AC边上， 
，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若
，求BDE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】李老师做了个长方形教具，其中一边长为2a+b，另一边长为a﹣b，则该长方形的面积为（ ）
A.6a+b
B.2a2﹣ab﹣b2
C.3a
D.10a﹣b
查看答案和解析>>
科目：初中数学 来源： 题型：
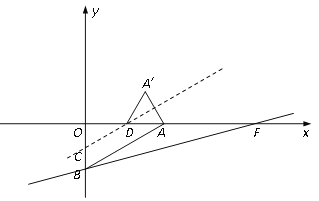
【题目】已知A（2
，0），直线y＝(2－
)x－2与x轴交于点F，与y轴交于点B，直线l∥AB且交y轴于点C，交x轴于点D，点A关于直线l的对称点为A′，连接AA′、A′D．直线l从AB出发，以每秒1个单位的速度沿y轴正方向向上平移，设移动时间为t．
（1）求点A′ 的坐标（用含t的代数式表示）；
（2）求证：AB＝AF；
（3）过点C作直线AB的垂线交直线y＝(2－
)x－2于点E，以点C为圆心CE为半径作⊙C，求当t为何值时，⊙C与△AA′D三边所在直线相切？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
