
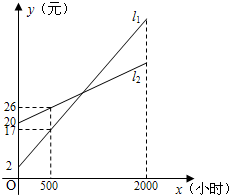
 如图所示,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图象,假设两种灯的使用寿命都是2000h,照明效果一样.
如图所示,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图象,假设两种灯的使用寿命都是2000h,照明效果一样.分析 (1)理由待定系数法,把问题转化为解方程组即可.
(2)根据题意列出方程即可解决问题.
(3)观察图象,可知17<26,由此即可判断.
解答 解析:(1)设L1的解析式为y1=k1x+b1,L2的解析式为y2=k2x+b2.
由图可知L1过点(0,2),(500,17),
∴$\left\{\begin{array}{l}2={b_1}\\ 17=500{k_1}+{b_1}\end{array}\right.$,
∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2000).
由图可知L2过点(0,20),(500,26),
同理y2=0.012x+20(0≤x≤2000)
(2)两种费用相等,即y1=y2,
则0.03x+2=0.012x+20,
解得x=1000.∴当x=1000时,两种灯的费用相等.
(3)用白炽灯,
理由:由图象可知,17<26,
∴y1<y2,
∴用白炽灯便宜.
点评 本题考查一次函数的应用、待定系数法,一元一次方程等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
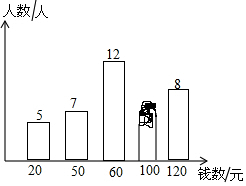 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com