Question

14．如图，平面直角坐标系中，已知点A（-3，0），B（0，4），对△AOB连续作旋转变换，依次得到三角形①，②，③，…，那么第2个三角形的直角顶点坐标是（$\frac{36}{5}$，$\frac{12}{5}$），第100个三角形的直角顶点坐标（396，0）．

Answer 1

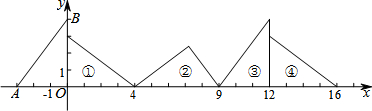
分析 先计算出AB，然后根据旋转的性质观察△OAB连续作旋转变换，得到△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，于是判断100个三角形和三角形④的状态一样，然后可计算出它的直角顶点的横坐标，从而得到100个三角形的直角顶点的坐标．

解答 解：∵点A（-3，0），B（0，4），
∴OB=4，OA=3，
∴AB$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵对△OAB连续作如图所示的旋转变换，
∴△OAB每三次旋转后回到原来的状态，并且每三次向前移动了3+4+5=12个单位，
而100=3×33+1，
∴第100个三角形Rt△₁₀₀和三角形④的状态一样，
所以第100个三角形的直角顶点的横坐标为33×12=396，纵坐标为0．
故答案为：（396，0）．

点评 本题考查了图形旋转后的坐标问题：先要理解所旋转图形的性质，然后根据旋转的性质理解每次旋转后图形各个点的坐标变化，从中找出变化的规律，再根据规律确定某种状态下的位置及坐标．