
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc<0;②b2-4ac<0;③3a+c<0;④m为任意实数,则m(am-b)+b≤a;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=-2,其中正确的有______(只填序号).
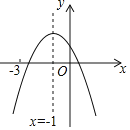
【答案】③④⑤.
【解析】
由抛物线对称轴的位置判断ab的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵抛物线的对称轴在y轴的左侧,
∴ab>0,
由图象可知:c>0,
∴abc>0,
故①错误;
②∵抛物线与x轴的交点有两个,
∴b2-4ac>0,②错误;
③∵![]() ,
,
∴b=2a,
由图象可知:9a-3b+c<0,
∴9a-6a+c<0,即3a+c<0,故③正确;
④∵抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2-bm+c≤a-b+c(m为任意实数),
∴m(am-b)≤a-b(m为任意实数),
∴m为任意实数,则m(am-b)+b≤a,所以④正确;
⑤∵对称轴x=-1,
∴x1≠x2,x1+x2=-2时,有ax12+bx1+c=ax22+bx2+c,
∴ax12+bx1=ax22+bx2,
∴结论⑤正确.
综合以上可得:③④⑤.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
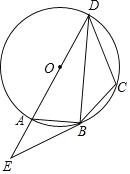
(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
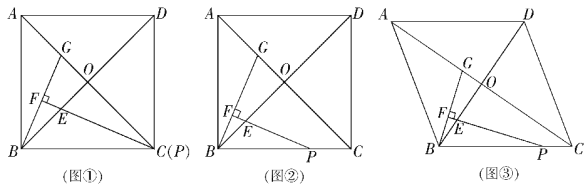
(1) 当点P与点C重合时(如图①).求证:△BOG≌△POE;(4分)
(2)通过观察、测量、猜想:![]() = ,并结合图②证明你的猜想;(5分)
= ,并结合图②证明你的猜想;(5分)
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求![]() 的值.(用含α的式子表示)(5分)
的值.(用含α的式子表示)(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
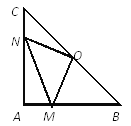
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线BD上,EF∥AB交AD于点F,连接BF.
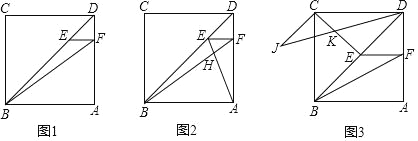
(1)如图1,若AB=4,DE=![]() ,求BF的长;
,求BF的长;
(2)如图2.连接AE,交BF于点H,若DF=HF=2,求线段AB的长;
(3)如图3,连接BF,AB=3![]() ,设EF=x,△BEF的面积为S,请用x的表达式表示S,并求出S的最大值;当S取得最大值时,连接CE,线段DB绕点D顺时针旋转30°得到线段DJ,DJ与CE交于点K,连接CJ,求证:CJ⊥CE.
,设EF=x,△BEF的面积为S,请用x的表达式表示S,并求出S的最大值;当S取得最大值时,连接CE,线段DB绕点D顺时针旋转30°得到线段DJ,DJ与CE交于点K,连接CJ,求证:CJ⊥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
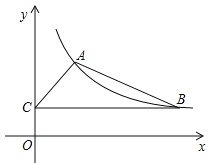
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com