
分析 (1)直接利用勾股定理得出x的值;
(2)利用(1)中分析得出x的取值范围;
(3)利用$\sqrt{2}$的近似值进而得出答案;
(4)利用$\sqrt{2}$的近似值进而得出答案.
解答 解:(1)x不是有理数.
理由:由勾股定理可知x2=42+42=32,首先x不可能是整数(因为52=25,62=36,所以x在5和6之间),
其次x也不可能是分数(因为若x是最简分数$\frac{n}{m}$,则($\frac{n}{m}$)2,仍是一个分数,不等于32),
综上可知:x既不是整数,也不是分数,所以x不是有理数;
(2)x在5和6之间;
(3)∵边长为4的正方形的对角线长为x,
∴x=4$\sqrt{2}$≈5.7;
(4)4$\sqrt{2}$≈4×1.414≈5.66.
点评 此题主要考查了估算无理数大小以及近似数,正确得出$\sqrt{2}$的近似值是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
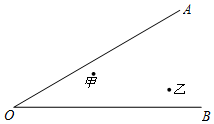 近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件:
近年来,国家实施农村医疗卫生改革,某县计划在甲村、乙村之问设立一座定点医疗站点P,甲、乙两村坐落在两相交公路内(如图所示).医疗站必须适合下列条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
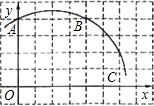 如图,已知直角坐标系中,A(0,4)、B(4,4)、C(6,2),
如图,已知直角坐标系中,A(0,4)、B(4,4)、C(6,2),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com