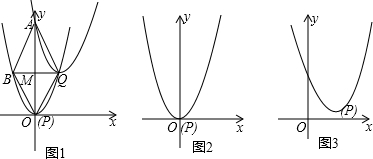
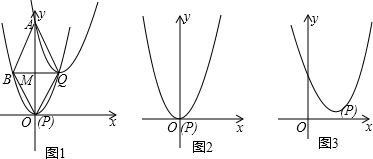
如图1,抛物线F1:y=x2的顶点为P,将抛物线F1平移得到抛物线F2,使抛物线F2的顶点Q始终在抛物线F1图象上(点Q不与点P重合),过点Q直线QB∥x轴,与抛物线F1的另一个交点为B,抛物线F1的对称轴交抛物线F2于点A.
(1)猜想四边形ABOQ的形状为______,若四边形ABOQ有一个内角为60°,则此时点Q的坐标为______
【答案】
分析:此题3个小题的解法是一致的,首先表示出平移后的抛物线解析式,易知AP垂直平分线段BQ,只需看BQ是否垂直平分AP即可,可将P点横坐标代入平移后的抛物线中,即可得到点A的坐标,然后比较AP的长是否为Q、P纵坐标差的2倍即可;
在证得四边形ABPQ是菱形后,设AP与BQ的交点为M,若菱形的一个内角为60°,那么△AMQ中,∠MAQ=30°或60°,AM、MQ的长可由点A、Q的坐标获得,根据AM=
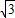
MQ或
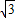
AM=MQ即可求得点Q的坐标.
解答:解:(1)设平移后的抛物线F
2的解析式为:y=(x-R)
2+S,(R>0,S>0),
由于F
2的顶点(R,S)在抛物线F
1的图象上,则有:
S=R
2,即抛物线F
2:y=(x-R)
2+R
2,
当x=0时,y=2R
2;
设AP与BQ的交点为M,则AM=PM=R
2,
所以AP、BQ互相垂直平分,
即四边形ABPQ是菱形;
由于菱形的一个内角是60°,则:
①△AMQ中,∠MAQ=30°时,AM=
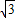
QM,
即R
2=
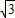
R,
解得R=
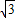
,此时Q(
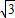
,3);
②△AMQ中,∠MAQ=60°时,
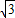
AM=QM,即
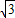
R
2=R,
解得R=
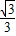
,此时Q(
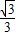
,

).
(2)设F
2:y=a(x-R)
2+S,(R>0,S>0),
同(1)可得:S=aR
2,
即抛物线F
2:y=a(x-R)
2+aR
2;
当x=0时,y=2aR
2;
即AM=PM=aR
2,故AP、BQ互相垂直平分,即四边形ABPQ是菱形;
若菱形的一个内角是60°,同(1)可知:
①AM=
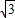
QM,即aR
2=
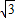
R,解得R=
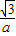
,此时Q(
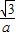
,
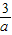
);
②
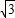
AM=QM,即
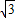
aR
2=R,解得R=
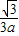
,此时Q(
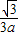
,
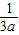
).
(3)设F
2:y=a(x-R)
2+S,(R>0,S>0),
同(2)得:S=a(R-m)
2+n,即抛物线F2:y=a(x-R)
2+a(R-m)
2+n,
当x=m时,y=2a(R-m)
2+n,
故AM=PM=a(R-m)
2,
同理可得四边形ABPQ是菱形;
Q(m+
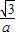
,n+
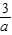
)或(m+
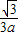
,n+

).
点评:此题主要考查了二次函数的性质以及菱形的判定方法,由于题目中大部分数据都是未知数,所以难度较大.

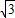 MQ或
MQ或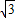 AM=MQ即可求得点Q的坐标.
AM=MQ即可求得点Q的坐标.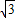 QM,
QM,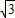 R,
R,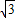 ,此时Q(
,此时Q(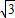 ,3);
,3);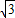 AM=QM,即
AM=QM,即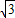 R2=R,
R2=R,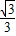 ,此时Q(
,此时Q(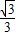 ,
, ).
).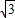 QM,即aR2=
QM,即aR2=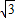 R,解得R=
R,解得R=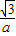 ,此时Q(
,此时Q(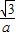 ,
,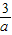 );
);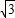 AM=QM,即
AM=QM,即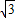 aR2=R,解得R=
aR2=R,解得R=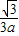 ,此时Q(
,此时Q(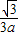 ,
,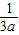 ).
).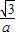 ,n+
,n+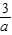 )或(m+
)或(m+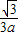 ,n+
,n+ ).
).

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案