
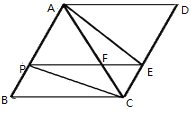
【题目】如图,在四边形ABCD中,![]() ,
,![]() ,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,
,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,![]()
![]() ,
,![]() .
.
(1)判断四边形PBCE的形状,并说明理由;
(2)求证:![]() ;
;
(3)当P为AB的中点时,四边形APCE是什么特殊四边形?请说明理由.
【答案】(1)四边形PBCE为平行四边形,证明过程见解析;(2)见解析;(3)四边形APCE为矩形,证明过程见解析.
【解析】
(1)证明四边形ABCD为平行四边形,从而得BP//CE,根据内错角相等证明AD//PE,从而可证PE//BC,得四边形PBCE为平行四边形;(2)证明△CBP≌△ACE即可证明CP=AE;(3)证明四边形APCE为平行四边形,然后根据三线合一证明∠APC=90°,可证四边形APCE为矩形.
解:(1)四边形PBCE为平行四边形.
证明:∵![]() ,
,![]() ,
,
∴四边形ABCD为平行四边形,
∴PB//EC,
∵![]() ,
,
∴AD//PE,
∴PE//BC,
∴四边形PBCE为平行四边形.
(2)∵四边形ABCD为平行四边形,
∴∠B=∠D,AB//CD,
∴![]()
又∵![]()
![]() ,
,
∴∠B=![]() ,
,
∴BC=AC,![]()
∵四边形PBCE为平行四边形,
∴PB=CE,
在△CBP和△ACE中

∴△CBP≌△ACE.
∴![]() .
.
(3)四边形APCE为矩形,
证明:∵P为AB的中点
∴BP=AP,
∵四边形PBCE为平行四边形,
∴BP=CE,
∴AP=CE,
又∵AB//CD
∴四边形APCE为平行四边形,
∵CB=CA,AP=BP,
∴CP⊥AB,
∴∠APC=90°,
∴![]() 为矩形.
为矩形.


科目:初中数学 来源: 题型:
【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和一体机,经过市场考察得知,购进 1 台笔记本电脑和 2 台一体机需要 1.45 万元,购进 2 台笔记本电脑和 1 台一体机需要 1.55 万元.
(1)求每台笔记本电脑、一体机各多少万元?
(2)根据学校实际,需购进笔记本电脑和一体机共35台,总费用不超过17.5万元,但不低于 17.2万元,请你通过计算求出共几种购买方案,并写出费用最低具体方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
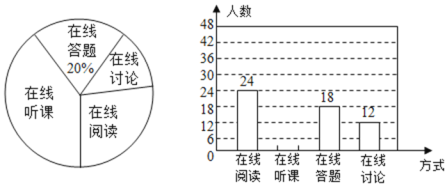
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D为AC的中点,过点C作
,点D为AC的中点,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取![]() ,连接BG、DF.
,连接BG、DF.
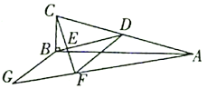
(1)证明:四边形BDFG是菱形;
(2)若![]() ,
,![]() ,求线段AG的长度.
,求线段AG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,
,![]() ,那么
,那么![]() 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
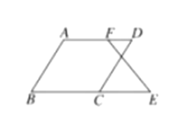
解:成立,理由如下:
![]() (已知)
(已知)
![]() ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)
![]() (② )
(② )
又![]()
![]() (已知),
(已知),![]() (等量代换)
(等量代换)
![]() (③ )
(③ )
![]() (④ ).
(④ ).
查看答案和解析>>
科目:初中数学 来源: 题型:
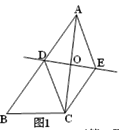
【题目】如图,已知△ABC,AC的垂直平分线交AB于点D,交AC于点O,过点C作CE∥AB交直线OD于点E,连接AE、CD.
⑴如图1,求证:四边形ADCE是菱形;
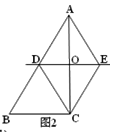
⑵如图2,当∠ACB=90°,BC=6,△ADC的周长为18时,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.
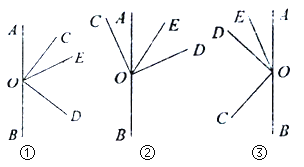
(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com