
 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABC的和EFGH都是正方形.根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=b,c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABC的和EFGH都是正方形.根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=b,c=10,a-b=2.分析 (1)先求出正方形边长,再根据正方形面积公式可求正方形EFGH的面积;根据面积的和差可求四个直角三角的面积和;
(2)根据完全平方公式可求(a+b)2的值.
(3)开方可求a+b,再与a-b=2联立可求a,b的值.
解答 解:(1)正方形EFGH的面积为(a-b)2=22=4,四个直角三角的面积和为102-4=100-4=96.
(2)(a+b)2
=a2+b2+2ab
=c2+2ab
=100+96
=196.
(3)a+b=$\sqrt{196}$=14①,
∵(a-b)2=22=4,
∴a-b=2②,
联立$\left\{\begin{array}{l}{a+b=14}\\{a-b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=8}\\{b=6}\end{array}\right.$.
故答案为:4,96;14,8,6.
点评 考查了勾股定理的证明,关键是应用直角三角形中勾股定理的运用解得a、b的值.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:填空题
 如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有①②④
如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有①②④查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
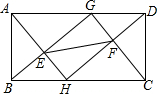 如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,
如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com