
 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.分析 (1)连接AD、OD,则AD⊥BC,D为BC中点.OD为中位线,则OD∥AC,根据DF⊥AC可得OD⊥DF.得证;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
解答 (1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC.
又AB=AC=13,BC=10,D是BC的中点,
∴BD=5.
连接OD;
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线;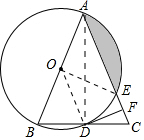
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8
∴S阴影=S扇形AOE-S△AOE=4π-8.
点评 本题考查切线的判定、等腰三角形的判定和性质、扇形的面积公式等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,学会用分割法求阴影部分面积,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.
如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是平行四边形ABCD的边BC上的三等分点,连接AE交对角线BD于点F,若△ADF的面积为18cm2,则S△ABF的面积是6cm2.
如图,点E是平行四边形ABCD的边BC上的三等分点,连接AE交对角线BD于点F,若△ADF的面积为18cm2,则S△ABF的面积是6cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全).
某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全). | 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 等级 | A | B | C | D |
| 学生人数 | m | 20 | n | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com