
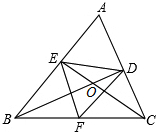
 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.分析 ①由EF和DF均是斜边BC边上的中线可迅速作出判断;
②由B、C、D、E四点共圆及割线定理迅速作出判断;
③由B、C、D、E四点共圆可得出对应圆周角相等,从而得出结论;
④若∠ABC=45°,则△BEC是等腰直角三角形,而F是BC中点,从而结论显然.
解答 解:∵BD⊥AC于点D,CE⊥AB于点E,F为BC的中点,
∴EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,
∴EF=DF,故①正确;
∵∠BEC=∠BDC=90°,
∴B、C、D、E四点共圆,
由割线定理可知AD•AC=AE•AB,故②正确;
∵B、C、D、E四点共圆,
∴∠OED=∠OBC,∠ODE=∠OCB,
∴△DOE∽△COB,故③正确;
若∠ABC=45°,则△BEC为等腰直角三角形,
∴BC=$\sqrt{2}$BE,
∵F为BC中点,
∴FC=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$BE,
∴BE=$\sqrt{2}$FC,故④正确;
故答案为:①②③④.
点评 本题主要考查了直角三角形斜边中线定理、四点共圆的判定与性质、割线定理、相似三角形的判定与性质、等腰直角三角形的判定与性质等知识点,难度不大,属于常规题型.解答的关键是明确题目所给条件(比如中点,垂直)与所学几何定理的联系.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
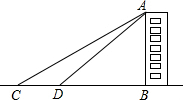 某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度.
某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
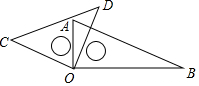 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA与∠DOA互余 | D. | ∠AOD与∠COB互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
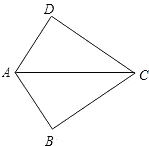 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BAC=∠DAC | ||
| C. | ∠BCA=∠DCA | D. | ∠B=∠D=90°,∠DAC=56°,∠BCA=34° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$S=ah | B. | 2S=ah | C. | S-h=$\frac{1}{2}$a | D. | $\frac{S}{2a}$=h |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
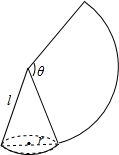 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com