

分析 (1)将x=2代入y=x中求出y值,由此即可得出点M的坐标;
(2)根据点M的坐标利用待定系数法即可求出一次函数解析式,再将y=0代入一次函数解析式中求出x值,由此即可得出点A的坐标;
(3)将x=0代入一次函数解析式求出y值,由此即可得出点B的坐标,进而可得出CD=OB=3,再根据一次函数解析式上点的坐标特征即可得出点C、D的坐标,利用两点间的距离公式即可得出关于a的一元一次方程,解之即可得出结论.
解答 解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,
∴y=x=2,
∴点M的坐标为(2,2).
(2)把M(2,2)代入y=-$\frac{1}{2}$x+b得:-1+b=2,
解得:b=3,
∴一次函数的解析式为y=-$\frac{1}{2}$x+3.
当y=-$\frac{1}{2}$x+3=0时,x=6,
∴A点坐标为(6,0).
(3)当x=0时,y=-$\frac{1}{2}$x+3=3,
∴点B的坐标为(0,3),
∴OB=3.
∵CD=OB,
∴CD=3.
∵PC⊥x轴,
∴点C的坐标为(a,-$\frac{1}{2}$a+3),点D的坐标为(a,a),
∴CD=a-(-$\frac{1}{2}$a+3)=3,
∴a=4.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及两点间的距离,解题的关键是:(1)将x=2代入y=x中求出y值;(2)根据点M的坐标利用待定系数法求出一次函数解析式;(2)根据两点间的距离列出关于a的一元一次方程.


科目:初中数学 来源: 题型:填空题
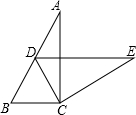 如图,在Rt△ABC中,∠ACB=90°,∠A=24°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,旋转角为48°.
如图,在Rt△ABC中,∠ACB=90°,∠A=24°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,旋转角为48°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
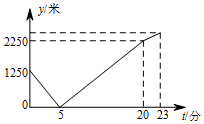 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△A1B1C1由△ABC绕某点旋转而成,请你用尺规作图,找出旋转中心O,并用量角器度量出旋转的大小(完成填空).旋转角(∠COC1)是90度.
如图,△A1B1C1由△ABC绕某点旋转而成,请你用尺规作图,找出旋转中心O,并用量角器度量出旋转的大小(完成填空).旋转角(∠COC1)是90度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com