
| A. | 2或-2 | B. | 2或6 | C. | 2 | D. | 3 |
分析 根据a、b互为相反数,可得a+b=0;根据c、d互为倒数,可得cd=1;根据x的绝对值是2,可得x=±2,x2=4,据此求出x2-cd•x+(a+b)2017的值是多少即可.
解答 解:∵a、b互为相反数,
∴a+b=0;
∵c、d互为倒数,
∴cd=1;
∵x的绝对值是2,
∴x=±2,x2=4,
∴当x=-2时,x2-cd•x+(a+b)2017=4+2+0=6;
当x=2时,x2-cd•x+(a+b)2017=4-2+0=2.
故选:B.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
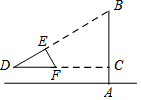 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )
如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )| A. | 一直增大 | B. | 一直不变 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 250×104 | B. | 2.5×105 | C. | 2.5×106 | D. | 2.5×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com