
如图,一次函数y=ax+b的图象与反比例函数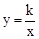 的图象交于A(﹣2,m),B
的图象交于A(﹣2,m),B
(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.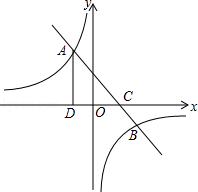
(1)求这两个函数的解析式:
(2)求△ADC的面积.
解:(1)∵反比例函数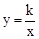 的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8。
的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8。
∴反比例函数的解析式为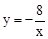 。
。
∵反比例函数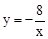 的图象过点A(﹣2,m),∴
的图象过点A(﹣2,m),∴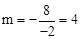 。∴A(﹣2,4)。
。∴A(﹣2,4)。
∵一次函数y=ax+b的图象过A(﹣2,4),B(4,﹣2)两点,
∴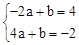 ,解得
,解得 。
。
∴一次函数的解析式为y=﹣x+2。
(2)∵直线AB:y=﹣x+2交x轴于点C,∴C(2,0)。
∵AD⊥x轴于D,A(﹣2,4),∴CD=2﹣(﹣2)=4,AD=4。
∴S△ADC=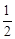 •CD•AD=
•CD•AD=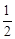 ×4×4=8。
×4×4=8。
解析试题分析:(1)因为反比例函数过A、B两点,所以可求其解析式和m的值,从而知A点坐标,进而求一次函数解析式。
(2)先求出直线AB与与x轴的交点C的坐标,再根据三角形的面积公式求解即可。


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数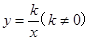 在第一象限内的交点.
在第一象限内的交点.
(1)求点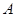 的坐标及
的坐标及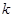 的值;
的值;
(2)试在 轴上确定一点
轴上确定一点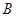 ,使
,使 ,求出点
,求出点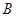 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数 的图象经过点C,一次函数
的图象经过点C,一次函数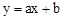 的图象经过点C,一次函数
的图象经过点C,一次函数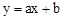 的图象经过点A,
的图象经过点A,
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点A(1,a)在反比例函数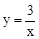 (x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数
(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数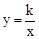 (x>0)的图象上.
(x>0)的图象上.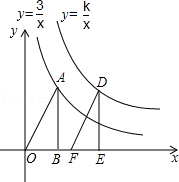
(1)求点A的坐标;
(2)求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数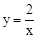 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).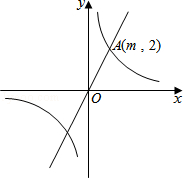
(1)求m的值;
(2)求正比例函数y=kx的解析式;
(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年广东梅州8分)已知,一次函数y=x+1的图象与反比例函数 的图象都经过点A(a,2).
的图象都经过点A(a,2).
(1)求a的值及反比例函数的表达式;
(2)判断点B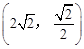 是否在该反比例函数的图象上,请说明理由.
是否在该反比例函数的图象上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=-x的图像与反比例函数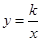 的图象交于A、B两点。
的图象交于A、B两点。
①根据图象求K的值
②点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,试写出点P所有可能的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,AB∥CD,AF交CD于点O,且OF平分∠EOD,如果∠A=34°,那么∠EOD的度数是( )
| A.34° | B.68° | C.102° | D.146° |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com