
【题目】如图,已知等边△ABC,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
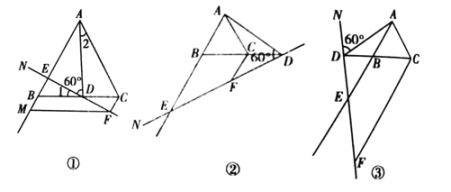
(1)当点D在线段BC上,∠NDB为锐角时,如图①.
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)①当点D在线段BC的延长线上,∠NDB为锐角时,如图②,请直接写出线段CF,BE,CD之间的数量关系;
②当点D在线段CB的延长线上,∠NDB为钝角或直角时,如图③,请直接写出线段CF,BE,CD之间的数量关系.
【答案】(1)①∠1=∠2,理由见解析,②证明见解析;(2)①BE=CD+CF,②CF=CD+BE.
【解析】
(1)①由等边三角形的性质和∠ADN=60°,易得∠1+∠ADC=120°,∠2+∠ADC=120°,所以∠1=∠2;
②由条件易得四边形BCFM为平行四边形,得到BM=CF,BC=MF,再证明△MEF≌△CDA,得到ME=CD,利用等量代换即可得证;
(2)①过F作FH∥BC,易得四边形BCFH为平行四边形,可得HF=BC,BH=CF,然后证明△EFH≌△DAC,得到CD=EH,利用等量代换即可得BE=CD+CF;
②过E作EG∥BC,易得四边形BCGE为平行四边形,可得EG=BC,BE=CG,然后证明△EFG≌△ADC,得到CD=FG,利用等量代换即可得CF=CD+BE.
(1)①∠1=∠2,理由如下:
∵△ABC为等边三角形
∴∠ACB=60°
∴∠2+∠ADC=120°
又∵∠AND=60°
∴∠1+∠ADC=120°
∴∠1=∠2
②∵MF∥BC,CF∥BM
∴四边形BCFM为平行四边形
∴BM=CF,BC=MF=AC,
∵BC∥MF
∴∠1=∠EFM=∠2,∠EMF=∠ABC=60°
在△MEF和△CDA中,
∵∠EFM=∠2,MF= AC,∠EMF=∠ACD=60°
∴△MEF≌△CDA(ASA)
∴ME=CD
∴ME=BM+BE=CF+BE=CD
即CF+BE=CD
(2)①BE=CD+CF,证明如下:
如图,过F作FH∥BC,
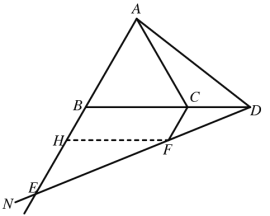
∵CF∥BH,FH∥BC,
∴四边形BCFH为平行四边形
∴HF=BC=AC,BH=CF
∵△ABC为等边三角形
∴∠ABC=∠ACB=60°
∴∠CAD+∠ADC=60°,∠DBE=120°,∠ACD=120°
又∵∠AND=60°,即∠BDN+∠ADC=60°
∴∠CAD=∠BDN
∵BD∥HF
∴∠HFE=∠BDN=∠CAD,∠EHF=∠ACD=120°
在△EFH和△DAC中,
∵∠EHF=∠ACD,HF=AC,∠HFE=∠CAD
∴△EFH≌△DAC(ASA)
∴EH=CD
∴BE=BH+EH=CF+CD
即BE=CD+CF;
②CF=CD+BE,证明如下:
如图所示,过E作EG∥BC,

∵EG∥BC,CG∥BE
∴四边形BCGE为平行四边形,
∴EG=BC=AC,BE=CG,
∵∠AND=60°,∠ACD=60°
∴∠ADC+∠CDE=120°,∠ADC+∠DAC=120°
∴∠CDE=∠DAC
又∵CD∥EG
∴∠GEF=∠CDE=∠DAC,∠EGF=∠DCF
∵AE∥CF
∴∠DCF=∠ABC=60°
∴∠EGF=∠ABC=60°
在△EFG和△ADC中,
∵∠GEF=∠DAC,EG=AC,∠EGF=∠ACD=60°
∴△EFG≌△ADC(ASA)
∴FG=CD
∴CF=CG+FG=BE+CD
即CF=CD+BE


科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
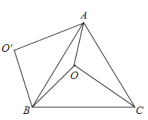
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转60°得到:②点
逆时针旋转60°得到:②点![]() 与
与![]() 的距离为4;③
的距离为4;③![]() ;④
;④![]() 四边形
四边形![]() ;⑤
;⑤![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③④B.①②③⑤C.①②④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为()
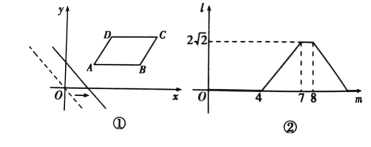
A.4B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是等腰直角三角形,动点
是等腰直角三角形,动点![]() 在斜边
在斜边![]() 所在的直线上,以
所在的直线上,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形![]() ,其中
,其中![]() ,探究并解决下列问题:
,探究并解决下列问题:
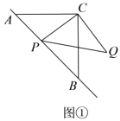
(1)如图①,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,则:
,则:
①![]() 长为
长为![]() ;
;![]() 的长为 ;
的长为 ;
②猜想:![]() ,
,![]() ,
,![]() 三者之间的数量关系为 ;
三者之间的数量关系为 ;
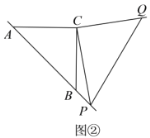
(2)如图②,若点![]() 在
在![]() 的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
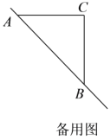
(3)若动点![]() 满足
满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() .例如,点
.例如,点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() ,即
,即![]()
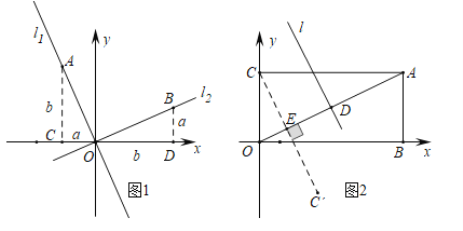
材料二:如图1,正比例函数![]() 和
和![]() 的图象相互垂直,分别在
的图象相互垂直,分别在![]() 和
和![]() 上取点
上取点![]() 、
、![]() 使得
使得![]() 分别过点
分别过点![]() 作
作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() .显然,
.显然,![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ..于是
..于是![]() ,
,![]() 所以
所以![]() 的值为一个常数,一般地,一次函数
的值为一个常数,一般地,一次函数![]() ,
,![]() 可分别由正比例函数
可分别由正比例函数![]() 平移得到.
平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数![]() ,
,![]() 的图象相互垂直,则
的图象相互垂直,则![]() 的值为一个常数.
的值为一个常数.
(1)在材料二中,![]() =______(写出这个常数具体的值)
=______(写出这个常数具体的值)
(2)如图2,在矩形![]() 中
中![]() ,点
,点![]() 是
是![]() 中点,用两段材料的结论,求点
中点,用两段材料的结论,求点![]() 的坐标和
的坐标和![]() 的垂直平分线
的垂直平分线![]() 的解析式;
的解析式;
(3)若点![]() 与点
与点![]() 关于
关于![]() 对称,用两段材料的结论,求点
对称,用两段材料的结论,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令![]() ,
,![]() .若
.若![]() ,则图中有_______个平行四边形(不添加别的辅助线);若
,则图中有_______个平行四边形(不添加别的辅助线);若![]() ,且四边形ABCD的面积为28,则四边形FGEH的面积为_______.
,且四边形ABCD的面积为28,则四边形FGEH的面积为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com