
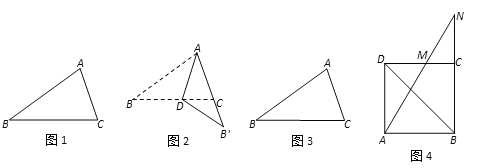
【题目】阅读材料:等腰三角形具有性质“等边对等角”.事实上,不等边三角形也具有类似性质“大边对大角”:如图1.在△ABC中,如果AB>AC,那么∠ACB>∠ABC.证明如下:将AB沿△ABC的角平分线AD翻折(如图2),因为AB>AC,所以点B落在AC的延长线上的点B'处.于是,由∠ACB>∠B',∠ABC=∠B',可得∠ACB>∠ABC.
(1)灵活运用:从上面的证法可以看出,折纸常常能为证明一个命题提供思路和方法.由此小明想到可用类似方法证明“大角对大边”:如图3.在△ABC中,如果∠ACB>∠ABC,那么AB>AC.小明的思路是:沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程.
(2)拓展延伸:请运用上述方法或结论解决如下问题:
如图4,已知M为正方形ABCD的边CD上一点(不含端点),连接AM并延长,交BC的延长线于点N.求证:AM+AN>2BD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)设BC的中垂线交BC于点E,交AB于点D,连接DC,结合中垂线的性质定理与三角形三边长的关系,即可得到结论;
(2)延长DC到点E,使得CE=CN,连接AE交BC于点F.易证△ACE≌△CAN,得AE=AN.过点C作PQ⊥AC,分别交AN、AE于点P、Q,结合“三角形中,大角对大边”,得AP+AQ>2AC,QE>CQ,PC>PM,进而得QE>PM,即AM+AN>AP+AQ,然后即可得到结论.
(1)设BC的中垂线交BC于点E,交AB于点D,连接DC.
将∠B沿BC的中垂线DE翻折(如图3),使点B落在点C处.
∵∠ACB>∠ABC,
∴CD在△ABC的内部,
∵DE为BC的中垂线,
∴DB=DC.
∵在△ADC中,AD+DC>AC,
∴AD+DB>AC.即AB>AC;
(2)如图4,延长DC到点E,使得CE=CN,连接AE交BC于点F.
∵∠ACE=∠ACN=135°,CE=CN,AC=AC,
∴△ACE≌△ACN(SAS),
∴AE=AN.
过点C作PQ⊥AC,分别交AN、AE于点P、Q.
∵∠ACP=∠ACQ=90°,
∴AP>AC,AQ>AC,
∴AP+AQ>2AC.
∵∠ACD>∠E,∠ACD=45°,∠QCE=135°-90°=45°,
∴∠QCE>∠E,
∴QE>CQ.
同理可得:PC>PM.
∵△ACE≌△ACN,
∴∠CAN=∠CAE,
又∵AC=AC,∠ACP=∠ACQ=90°,
∴△ACP≌△ACQ(ASA),
∴PC=CQ,
∴QE>PM,
∴AM+AN=AM+AE=AM+AQ+QE>AM+AQ+PM=AP+AQ.
又∵AP+AQ>2AC,
∴AM+AN>2AC.
∵正方形ABCD中,AC=BD,
∴AM+AN>2BD.



 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
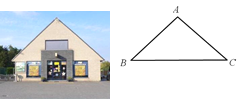
【题目】等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”“10元”“20元”“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出2个小球(第一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①等弧所对的圆心角相等;②90°的圆周角所对的弦是直径;③关于x的一元二次方程![]() 有两个不相等的实数根,则ac< 0;④若二次函数y=
有两个不相等的实数根,则ac< 0;④若二次函数y= ![]() 的图象上有两点(-1,y1)、(2,y2),则
的图象上有两点(-1,y1)、(2,y2),则![]() >
>![]() ;其中真命题的个数是( )
;其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
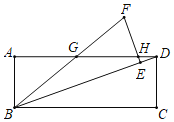
【题目】如图,矩形ABCD中,将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上.BF,EF分别交边AD于点G,H.若GH=4HD,则cos∠DBC的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
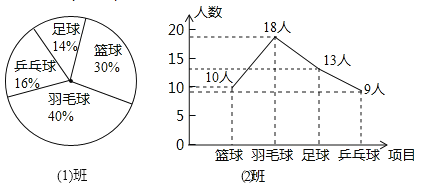
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜丰水果店计划用![]() 元/盒的进价购进一款水果礼盒以备销售.
元/盒的进价购进一款水果礼盒以备销售.
![]() 据调查,当该种水果礼盒的售价为
据调查,当该种水果礼盒的售价为![]() 元/盒时,月销量为
元/盒时,月销量为![]() 盒,每盒售价每增长
盒,每盒售价每增长![]() 元,月销量就相应减少
元,月销量就相应减少![]() 盒,若使水果礼盒的月销量不低于
盒,若使水果礼盒的月销量不低于![]() 盒,每盒售价应不高 于多少元?
盒,每盒售价应不高 于多少元?
![]() 在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了
在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了![]() ,而每盒 水果礼盒的售价比
,而每盒 水果礼盒的售价比![]() 中最高售价减少了
中最高售价减少了![]()
![]() ,月销量比
,月销量比![]() 中最低月销量
中最低月销量![]() 盒增加了
盒增加了![]() ,结果该月水果店销售该水果礼盒的利润达到了
,结果该月水果店销售该水果礼盒的利润达到了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
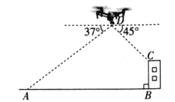
【题目】西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点![]() 处,操控者站在点
处,操控者站在点![]() 处,无人机测得点
处,无人机测得点![]() 的俯角为
的俯角为![]() ,测得教学楼楼顶点
,测得教学楼楼顶点![]() 处的俯角为
处的俯角为![]() .又经过人工测量得到操控者和教学楼
.又经过人工测量得到操控者和教学楼![]() 的距离为57米,求教学楼
的距离为57米,求教学楼![]() 的高度.(注:点
的高度.(注:点![]() 都在同一平面上,无人机大小忽略不计.参考数据:
都在同一平面上,无人机大小忽略不计.参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com