
 如图所示,△ABC中,∠ACB=90°,CD是高,AE是角平分线,交CD于F,EG⊥AB,G是垂足,求证:四边形CEGF是菱形.
如图所示,△ABC中,∠ACB=90°,CD是高,AE是角平分线,交CD于F,EG⊥AB,G是垂足,求证:四边形CEGF是菱形. 分析 首先利用角平分线的性质证明CE=EG,然后证明△CEF≌△GEF,则FG=FC,根据等角对等边证明CF=CE,从而得到四边形CEGF四边相等,则四边形是菱形.
解答 证明:∵AE平分∠BAC交CD于F,
∴CE=EG,∠AEG=∠AEC,
在△CEF和△GEF中,
$\left\{\begin{array}{l}{GE=CE}\\{∠AEG=∠AEC}\\{EF=EF}\end{array}\right.$,
∴△CEF≌△GEF(SAS),
∴FG=FC,∠CFE=∠GFE,
∵CD⊥AB,EG⊥AB,
∴CD∥EG,
∴∠CFE=∠GEF,
又∵∠CFE=∠GFE,
∴∠CFE=∠CEF,
∴CF=CE,
又∵FG=FC,CE=EG,
∴CF=CE=EG=FG,
∴四边形CEGF是菱形.
点评 本题考查了平行四边形的性质和判定,菱形的判定,勾股定理,全等三角形的性质和判定的应用,通过做此题培养了学生的推理能力,题目比较好,综合性也比较强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
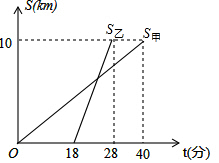 甲、乙两位教师先后从学校出发,到距学校10千米的培训中心参加新教材培训学习,图中S甲、S乙分别表示甲、乙两位教师从学校到培训中心所走的路程s(千米)随时间t(分钟)变化的函数图象.求乙出发后追上甲所用的时间是多少?
甲、乙两位教师先后从学校出发,到距学校10千米的培训中心参加新教材培训学习,图中S甲、S乙分别表示甲、乙两位教师从学校到培训中心所走的路程s(千米)随时间t(分钟)变化的函数图象.求乙出发后追上甲所用的时间是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各有一个角等于45°的两个等腰三角形 | |
| B. | 各有一个角等于60°的两个等腰三角形 | |
| C. | 两个等腰直角三角形 | |
| D. | 各有一个角等于105°的两个等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com