
分析 (1)根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据利润=1盒粽子所获得的利润×销售量列式整理,再根据二次函数的最值问题解答;
(3)先由(2)中所求得的P与x的函数关系式,根据每天销售粽子的利润不低于6000元,求出x的取值范围,再根据(1)中所求得的销售量y(盒)与每盒售价x(元)之间的函数关系式即可求解.
解答 解:(1)由题意得,y=700-20(x-45)=-20x+1600;
(2)P=(x-40)(-20x+1600)=-20x2+2400x-64000=-20(x-60)2+8000,
∵x≥45,a=-20<0,
∴当x=60时,P最大值=8000元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得-20(x-60)2+8000=6000,
解得x1=50,x2=70,
∵定价高于45元时,价格增加,销量减少,尽量减少库存,
∴定价为50元,
∴700-20(50-45)=600(盒),
答:要保证超市每天的利润不少于6000元,又要尽量减少库存,超市每天最多可以销售出600盒粽子.
点评 本题考查的是二次函数与一次函数在实际生活中的应用,主要利用了利润=1盒粽子所获得的利润×销售量,求函数的最值时,注意自变量的取值范围.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
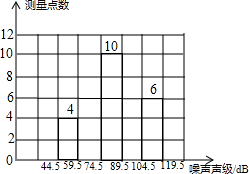 为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:
为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5-59.5 | 4 | 0.1 |
| 2 | 59.5-74.5 | a | 0.2 |
| 3 | 74.5-89.5 | 10 | 0.25 |
| 4 | 89.5-104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
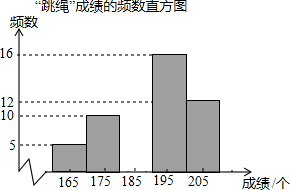 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:| 组别 | 组中值(个) | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | C | D | |
| A | ||||
| B | ||||
| C | ||||
| D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com