

分析 (1)先过D作DE⊥AB,过N作NF⊥AB,根据NF∥DE,得出$\frac{NF}{DE}$=$\frac{AN}{AD}$=$\frac{AF}{AE}$,求得NF=3$\sqrt{3}$,AF=3,在Rt△MNF中,根据MN=$\sqrt{N{F}^{2}+F{M}^{2}}$进行计算即可;
(2)先求得梯形ABCD的面积=$\frac{(8+12)×4\sqrt{3}}{2}$=40$\sqrt{3}$,再分两种情况:①当0≤t≤4时,则BM=12-3t,CN=2t,②当4<t≤8时,则AM=24-3t,AN=16-2t,分别根据MN将四边形ABCD的面积分为相等的两个部分,列方程求解即可;
(3)分两种情况讨论:①当0≤t≤4时,则AM=3t,CN=2t;②当4<t≤8时,分别延长CD、MN交于点Q,则AM=24-3t,AN=16-2t,DN=2t-8.分别根据AB∥CD,列出比例式进行求解即可.
解答 解:(1)如图所示,当t=5(s)时,点N移动的路程为10,点M移动的路程为15,
∴点N在AD上,DN=10-8=2,点M在AB上,BM=15-12=3,
∴AN=6,AM=9,
过D作DE⊥AB,过N作NF⊥AB,则BE=CD=8,AE=12=8=4,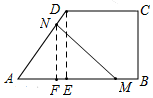
∴Rt△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=4$\sqrt{3}$,
∵NF∥DE,
∴$\frac{NF}{DE}$=$\frac{AN}{AD}$=$\frac{AF}{AE}$,即$\frac{NF}{4\sqrt{3}}$=$\frac{6}{8}$=$\frac{AF}{4}$,
∴NF=3$\sqrt{3}$,AF=3,
∴FM=9-3=6,
∴Rt△MNF中,MN=$\sqrt{N{F}^{2}+F{M}^{2}}$=$\sqrt{63}$=3$\sqrt{7}$,
故答案为:3$\sqrt{7}$;
(2)∵四边形中ABCD中,AB∥CD,BC⊥AB,AD=CD=8cm,AB=12cm,
而BC=4$\sqrt{3}$,则梯形ABCD的面积=$\frac{(8+12)×4\sqrt{3}}{2}$=40$\sqrt{3}$.
①当0≤t≤4时,如图,则BM=12-3t,CN=2t,
∴梯形BCNM的面积=$\frac{1}{2}$(12-t)4$\sqrt{3}$=2$\sqrt{3}$(12-t),
∵MN将四边形ABCD的面积分为相等的两个部分,
∴2$\sqrt{3}$(12-t)=20$\sqrt{3}$,
∴t=2.
②当4<t≤8时,如图,则AM=24-3t,AN=16-2t,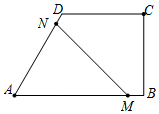
∴△AMN的面积=$\frac{1}{2}$×(24-3t)×$\frac{\sqrt{3}}{2}$(16-2t)=$\frac{3\sqrt{3}}{2}$(8-t)2,
∵MN将四边形ABCD的面积分为相等的两个部分,
∴$\frac{3\sqrt{3}}{2}$(8-t)2=20$\sqrt{3}$,
∴t=8±$\frac{2\sqrt{30}}{3}$,
又∵4<t≤8,
∴t=8-$\frac{2\sqrt{30}}{3}$,
综上所述:或t=2或8-$\frac{2\sqrt{30}}{3}$.
(3)①当0≤t≤4时,如图,则AM=3t,CN=2t.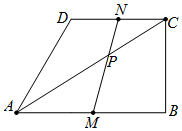
∵AB∥CD,
∴$\frac{AP}{PC}$=$\frac{AM}{CN}$=$\frac{3}{2}$≠$\frac{1}{2}$,
∴不存在符合条件的t值.
②当4<t≤8时,如图,分别延长CD、MN交于点Q.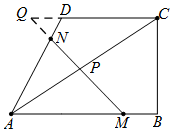
则AM=24-3t,AN=16-2t,DN=2t-8.
∵AB∥CD,
∴$\frac{QD}{AM}$=$\frac{DN}{AN}$,即$\frac{DQ}{24-3t}$=$\frac{2t-8}{16-2t}$,
解得DQ=3(t-4),
∴CQ=3t-4.
∵AB∥CD,
∴$\frac{AM}{CQ}$=$\frac{AP}{PC}$,即$\frac{24-3t}{3t-4}$=$\frac{1}{2}$,
解得t=$\frac{52}{9}$,
综上可知:存在实数t=$\frac{52}{9}$使得AP:PC=1:2成立.
点评 本题属于四边形综合题,主要考查了梯形的面积,勾股定理,平行线分线段成比例以及解一元二次方程的综合应用,解决问题的关键是作辅助线构造直角三角形,运用分类思想进行求解.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2(x-1)2-3 | B. | y=2(x+1)2-3 | C. | y=2(x-1)2+3 | D. | y=2(x+1)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查一批电脑的使用寿命情况 | |
| B. | 调查全国足球迷的身体健康状况 | |
| C. | 调查重庆市中小学生课外阅读情况 | |
| D. | 为保证“神州十一号”载人飞船的成功发射,对其零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 零 | D. | 非负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b<m<n | B. | b<a<n<m | C. | a<m<n<b | D. | m<a<b<n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
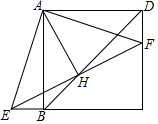 已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF
已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com