
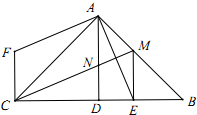
 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.分析 (1)两次运用同角的余角相等证明△AEB≌△AFC,得BE=CF;
(2)①过E作EH⊥AB于H,分别证明△BEH和△MEH是等腰直角三角形即可,
②根据HL证明Rt△ACM≌Rt△ECM,可以得出结论,或利用角平分线性质定理的逆定理证明更简单;
③证明△ADE≌△CDN,则DN=DE.
解答 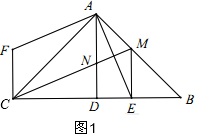 证明:(1)∵AE⊥AF,
证明:(1)∵AE⊥AF,
∴∠FAC+∠CAE=90°,
∵∠BAC=90°,
∴∠BAE+∠CAE=90°,∠B+∠ACB=90°,
∴∠FAC=∠BAE,
∵FC⊥CE,
∴∠FCA+∠ACB=90°,
∴∠FCA=∠B,
∵AC=AB,
∴△AEB≌△AFC,
∴BE=CF;
(2)①过E作EH⊥AB于H,则△BEH是等腰直角三角形,
∴HE=BH,∠BEH=45°,
∵AE平分∠BAD,AD⊥BC,
∴DE=EH,
∴DE=BH=HE,
∵BM=2DE,
∴HE=HM,
∴△HEM是等腰直角三角形,
∴∠MEH=45°,
∴∠BEM=45°+45°=90°,
∴ME⊥BC;
②∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵ME⊥BC,AD⊥BC,
∴ME∥AD,
∴∠MEA=∠DAE,
∴∠MEA=∠MAE,
∴AM=EM,
∵CM=CM,
∴Rt△ACM≌Rt△ECM,
∴∠ACM=∠ECM,
∴CM平分∠ACB;
③∵AE平分∠BAD,∠BAD=45°,
∴∠DAE=22.5°,
同理∠DCN=22.5°,
∴∠DAE=∠DCN,
∵∠ACD=∠CAD=45°,
∴AD=CD,
∵∠ADE=∠NDC=90°,
∴△ADE≌△CDN,
∴DN=DE.
点评 本题考查了三角形全等、等腰直角三角形的性质和判定,证明边和角相等时,一般就证明边和角所在的三角形全等即可,本题中有多个等腰直角三角形,利用45°角的和证明垂直的关系.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -6 | 6 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A=36°,∠ABC=∠ACB
如图,在△ABC中,∠A=36°,∠ABC=∠ACB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com