
如下图所示,二次函数图象的顶点坐标为C(2,-1),二次函数的图象在x轴上截得的线段AB的长为2.
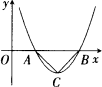
(1)求证:△ACB是等腰直角三角形;
(2)求二次函数的解析式;
(3)在抛物线上是否存在点P,使△PAC是等腰三角形,若存在,请求出点P的坐标,不能求出时,请给出横纵坐标的范围;若不存在,请说明理由.
|
(1)过点C作CD⊥AB于点D,∵AB=2,点C坐标为(2,-1),由二次函数的对称性可知A,B两点的坐标分别为A(1,0),B(3,0),故DA=DB=DC=1,∴△ACB是等腰直角三角形. (2)设抛物线的解析式为y=a(x-2)2-1,将(1,0)代入得a=1,故y=(x-2)2-1. (3)在抛物线上存在四点P,使△PAC是等腰三角形.①当AC为腰时,点B即为其中一个所求的点P3(3,0),∵AC= |
|
由抛物线的对称轴易证△ACB是等腰直角三角形.最后一问是开放性探索题,满足条件的P点有多个,可分AC为腰和AC为底两种情形进行求解. |


科目:初中数学 来源: 题型:
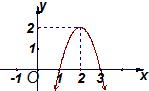 (1)函数值y有最
(1)函数值y有最查看答案和解析>>
科目:初中数学 来源: 题型:
 某精品水果超市销售一种进口水果A,从去年1至7月,这种水果的进价一路攀升,每千克A的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表:
某精品水果超市销售一种进口水果A,从去年1至7月,这种水果的进价一路攀升,每千克A的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y1(元/千克) | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如下图所示的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题.
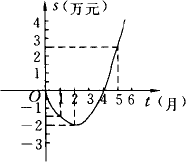
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com