
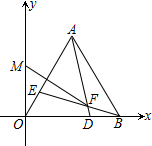
 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
分析 先判断出△OBE≌△DAB(SAS),即可判断出∠AFB=120°,即可判断出点F是以O'为圆心的圆上的一段弧(劣弧$\widehat{AB}$),然后确定出圆心O'的位置及坐标,设出点M的坐标,即可确定当点M(0,2$\sqrt{3}$)时,FM的最小值是6-2$\sqrt{3}$.
解答 解:如图, ∵△OAB是等边三角形,
∵△OAB是等边三角形,
∴∠AOB=∠ABD=60°,OB=AB,
∵点D、E分别从B、O以相同的速度向O、A运动,
∴BD=OE,在△OBE和△DAB中,$\left\{\begin{array}{l}{OE=BD}\\{∠BOE=∠ABD=60°}\\{OB=AB}\end{array}\right.$,
∴△OBE≌△DAB(SAS),
∴∠OBE=∠BAD,
∴∠ABE+∠BAD=∠ABE+∠OBE=∠ABO=60°
∴∠AFB=180°-(∠ABE+∠BAD)=120°,
∴点F是经过点A,B,F的圆上的点,记圆心为O',在⊙O'上取一点N,使点N和点F在弦AB的两侧,连接AN,BN,
∴∠ANB=180°-∠AFB=60°,
连接O'A,O'B,
∴∠AO'B=2∠ANB=120°,
∵O'A=O'B,
∴∠ABO'=∠BAO',
∴∠ABO'=$\frac{1}{2}$(180°-∠AO'B)=$\frac{1}{2}$(180°-120°)=30°,
∵∠ABO=60°,
∴∠OBO'=90°,
∵△AOB是等边三角形,A(3,m),
∴AB=OB=2×3,m=3$\sqrt{3}$,
过点O'作O'G⊥AB,
∴BG=$\frac{1}{2}$AB=3,
在Rt△BO'G中,∠ABO'=30°,BG=3,
∴O'B=$\frac{BG}{cos∠ABO'}$=$\frac{3}{cos30°}$=2$\sqrt{3}$,
∴O'(6,2$\sqrt{3}$),
设M(0,n),
∴O'M=$\sqrt{36+(n-2\sqrt{3})^{2}}$
∴FM=O'M-O'F=$\sqrt{36+(n-2\sqrt{3})^{2}}$-2$\sqrt{3}$,
只有n-2$\sqrt{3}$=0时,(n-2$\sqrt{3}$)2最小为0,即$\sqrt{36+(n-2\sqrt{3})^{2}}$最小为6.
当n-2$\sqrt{3}$=0时,即:n=2$\sqrt{3}$时,FM最小,
∴FM的最小值=6-2$\sqrt{3}$.
故选D.
点评 此题是圆的综合题,主要考查了等边三角形的性质,全等三角形的性质和判定,勾股定理等知识点;找出点F的运动轨迹是解本题的关键也是难点,是一道很好的定弦定角最值问题.解此类题目的方法是判断出动点的轨迹所在的圆的圆心和确定出半径.


科目:初中数学 来源: 题型:解答题
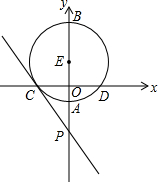 如图,在平面直角坐标系中,以E(0,1)为圆心,3为半径的⊙E交y轴于A、B两点,交x轴于C、D两点,点P的坐标为(0,-8)
如图,在平面直角坐标系中,以E(0,1)为圆心,3为半径的⊙E交y轴于A、B两点,交x轴于C、D两点,点P的坐标为(0,-8)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
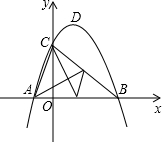 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(A,B分别在原点的左右两侧),与y轴交于点C,抛物线的顶点为点D,且OA:OB:OC=1:3:3,求抛物线的解析式及顶点D的坐标.
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(A,B分别在原点的左右两侧),与y轴交于点C,抛物线的顶点为点D,且OA:OB:OC=1:3:3,求抛物线的解析式及顶点D的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程(千米) | 0<x≤3 | 3<x≤6 | x>6 |
| 价格 | N元 | $\frac{22}{N}$元/千米 | $\frac{25}{N}$元/千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com