
如图,两个反比例函数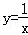 和
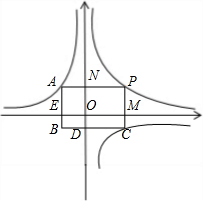
和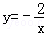 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )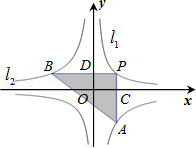
| A.3 | B.4 | C.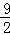 | D.5 |
C
解析试题分析:设P的坐标是(a, ),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.
),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.
解:∵点P在y= 上,
上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a, )(a为正数),
)(a为正数),
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=﹣ 上,
上,
∴A的坐标是(a,﹣ ),
),
∵PB⊥y轴,
∴B的纵坐标是 ,
,
∵B在y=﹣ 上,
上,
∴代入得: =﹣
=﹣ ,
,
解得:x=﹣2a,
∴B的坐标是(﹣2a, ),
),
∴PA=| ﹣(﹣
﹣(﹣ )|=
)|=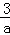 ,PB=|a﹣(﹣2a)|=3a,
,PB=|a﹣(﹣2a)|=3a,
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是: PA×PB=
PA×PB= ×
×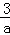 ×3a=
×3a= .
.
故选C.
考点:反比例函数综合题;三角形的面积.
点评:本题考查了反比例函数和三角形面积公式的应用,关键是能根据P点的坐标得出A、B的坐标,本题具有一定的代表性,是一道比较好的题目.


科目:初中数学 来源: 题型:
 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•德州)如图,两个反比例函数y=
(2012•德州)如图,两个反比例函数y=| 1 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,两个反比例函数y=
如图,两个反比例函数y=| 1 |
| x |
| 2 |
| x |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 2 |
| x |
| 3 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com