
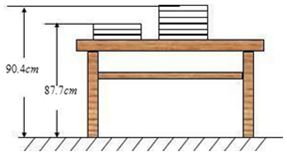
分析 (1)由于课桌的高度和每本书的厚度都为定值,可设这两个量为未知数,列出二元一次方程组求解.这摞课本距离地面的最大高度为:课桌高度+x本书的高度.
(2)把x=70-18代入(1)中式子即可求得.
解答 解:(1)设课桌的高度为acm,每本书的厚度为bcm.
则$\left\{\begin{array}{l}{3b+a=87.7}\\{6b+a=90.4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=85}\\{b=0.9}\end{array}\right.$.
故这摞课本距离地面的最大高度为85+0.9x.
(2)当x=70-18时,85+0.9x=131.8(cm).
答:余下的一摞课本距离地面的最大高度是131.8cm.
点评 考查了二元一次方程组的应用,解决本题需先求得课桌的高度和每本书的厚度,找到相应的等量关系是解决本题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
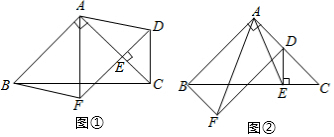
 如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自动铅笔(单位:支) | 笔记本(单位:本) | 总销售额(元) | |
| A | 20 | 32 | 72 |
| B | 10 | 36 | 56 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com