
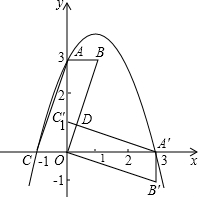
 (2012•龙岩质检)在平面直角坐标系中,ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),
(2012•龙岩质检)在平面直角坐标系中,ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),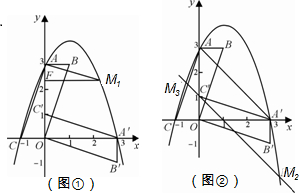 解:(1)由旋转不变性可知点A'(3,0),OA'=OA=3
解:(1)由旋转不变性可知点A'(3,0),OA'=OA=3| 2 |
| 2×(-1) |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| AF |
| C′O |
| FM |
| OA′ |
| m2-2m |
| 1 |
| m |
| 3 |
| 7 |
| 3 |
| 7 |
| 3 |
| 20 |
| 9 |
3±
| ||
| 2 |
3+
| ||
| 2 |
-1-
| ||
| 2 |
3-
| ||
| 2 |
-1+
| ||
| 2 |
| 7 |
| 3 |
| 20 |
| 9 |
3+
| ||
| 2 |
-1-
| ||
| 2 |
3-
| ||
| 2 |
-1+
| ||
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com