Question

设点M在正三角形三条高线上的射影分别是M₁，M₂，M₃（互不重合）．求证：△M₁M₂M₃也是正三角形．

Answer 1

分析：先根据题意画出图形，由等边三角形三线合一的性质可知M₁M₂=M₂M₃=M₁M₃，故可求出结论．

解答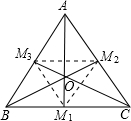：解：如图所示，
∵△ABC是等边三角形，AM₁⊥BC，BM₂⊥AC，CM₃⊥AB，
∴M₁、M₂、M₃分别是BC，AC，AB的中点，
∴M₁M₂、M₂M₃、M₁M₃是△ABC的中位线，
∴M₁M₂=M₂M₃=M₁M₃=

1

2

AB，
∴△M₁M₂M₃是正三角形．

点评：本题考查的是等边三角形的性质及三角形中位线定理，熟知等边三角形三线合一的性质是解答此题的关键．