
вбжЊХзЮяЯп ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ
ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ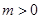 ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЈ1ЃЉЧѓmЕФжЕЃЌВЂНЋЦНвЦКѓЕФХзЮяЯпНтЮіЪНаДГЩ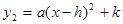 ЕФаЮЪНЃЛ
ЕФаЮЪНЃЛ
ЃЈ2ЃЉНЋЦНвЦКѓЕФХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЕНxжсЩЯЗНЃЌгыЦНвЦКѓЕФХзЮяЯпУЛгаБфЛЏЕФВПЗжЙЙГЩвЛИіаТЕФЭМЯѓ. ЧыаДГіетИіЭМЯѓЖдгІЕФКЏЪ§yЕФНтЮіЪНЃЌЭЌЪБаДГіИУКЏЪ§дк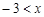 Ём
Ём ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшвЛДЮКЏЪ§ ЃЌЮЪЪЧЗёДцдке§ећЪ§
ЃЌЮЪЪЧЗёДцдке§ећЪ§ ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ
ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ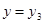 ЪБЃЌЖдгІЕФxЕФжЕЮЊ
ЪБЃЌЖдгІЕФxЕФжЕЮЊ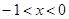 ЃЌШєДцдкЃЌЧѓГі
ЃЌШєДцдкЃЌЧѓГі ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.

НтЃКЃЈ1ЃЉгЩЬтвтПЩЕУ
гжЕуЃЈ1ЃЌ8ЃЉдкЭМЯѓЩЯ
Ёр 
Ёр m=2
Ёр 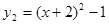
ЃЈ2ЃЉ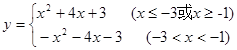
ЕБ ЪБЃЌ
ЪБЃЌ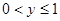
ЃЈ3ЃЉВЛДцдк
РэгЩЃКЕБy=y3ЧвЖдгІЕФ-1<x<0ЪБЃЌ
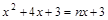
Ёр  ЃЌ
ЃЌ
Чв ЕУ
ЕУ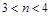
Ёр ВЛДцдке§ећЪ§nТњзуЬѕМў
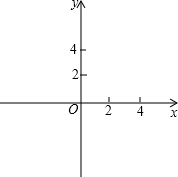
ЁОНтЮіЁПЃЈ1ЃЉИљОнХзЮяЯпy1=x2+4x+1ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЌПЩЕУy2=x2+4x+1+mЃЌдйРћгУгжЕуЃЈ1ЃЌ8ЃЉдкЭМЯѓЩЯЃЌЧѓГіmМДПЩЃЛ
ЃЈ2ЃЉИљОнКЏЪ§НтЮіЪНЛГіЭМЯѓЃЌМДПЩЕУГіКЏЪ§ДѓаЁЗжНчЕуЃЛ
ЃЈ3ЃЉИљОнЕБy=y3ЧвЖдгІЕФЉ1ЃМxЃМ0ЪБЃЌx2+4x+3=nx+3ЃЌЕУГіnШЁжЕЗЖЮЇМДПЩЕУГіД№АИЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 вбжЊЃКХзЮяЯпy=ЃЈm-1ЃЉx2+mx+m2-4ЕФЭМЯѓОЙ§дЕуЃЌЧвПЊПкЯђЩЯЃЎ
вбжЊЃКХзЮяЯпy=ЃЈm-1ЃЉx2+mx+m2-4ЕФЭМЯѓОЙ§дЕуЃЌЧвПЊПкЯђЩЯЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 3 | 2 |
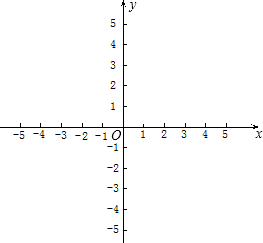 Ъ§ЕФКЏЪ§жЕy=y3ЪБЃЌЖдгІЕФxЕФжЕЮЊ-1ЃМxЃМ0ЃПШєДцдкЃЌЧѓГіnЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
Ъ§ЕФКЏЪ§жЕy=y3ЪБЃЌЖдгІЕФxЕФжЕЮЊ-1ЃМxЃМ0ЃПШєДцдкЃЌЧѓГіnЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2012НьББОЉЪаУХЭЗЙЕЧјОХФъМЖЩЯбЇЦкЦкФЉПМЪдЪ§бЇЪдОэЃЈДјНтЮіЃЉ ЬтаЭЃКНтД№Ьт
вбжЊХзЮяЯп ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ
ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ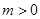 ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЈ1ЃЉЧѓmЕФжЕЃЌВЂНЋЦНвЦКѓЕФХзЮяЯпНтЮіЪНаДГЩ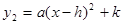 ЕФаЮЪНЃЛ
ЕФаЮЪНЃЛ
ЃЈ2ЃЉНЋЦНвЦКѓЕФХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЕНxжсЩЯЗНЃЌгыЦНвЦКѓЕФХзЮяЯпУЛгаБфЛЏЕФВПЗжЙЙГЩвЛИіаТЕФЭМЯѓ. ЧыаДГіетИіЭМЯѓЖдгІЕФКЏЪ§yЕФНтЮіЪНЃЌЭЌЪБаДГіИУКЏЪ§дк Ём
Ём ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшвЛДЮКЏЪ§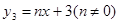 ЃЌЮЪЪЧЗёДцдке§ећЪ§
ЃЌЮЪЪЧЗёДцдке§ећЪ§ ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ
ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ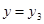 ЪБЃЌЖдгІЕФxЕФжЕЮЊ
ЪБЃЌЖдгІЕФxЕФжЕЮЊ ЃЌШєДцдкЃЌЧѓГі
ЃЌШєДцдкЃЌЧѓГі ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊХзЮяЯп![]() ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ
ЕФЭМЯѓЯђЩЯЦНвЦmИіЕЅЮЛЃЈ![]() ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЉЕУЕНЕФаТХзЮяЯпЙ§ЕуЃЈ1ЃЌ8ЃЉ.
ЃЈ1ЃЉЧѓmЕФжЕЃЌВЂНЋЦНвЦКѓЕФХзЮяЯпНтЮіЪНаДГЩ![]() ЕФаЮЪНЃЛ
ЕФаЮЪНЃЛ
ЃЈ2ЃЉНЋЦНвЦКѓЕФХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЕНxжс![]() ЩЯЗНЃЌгыЦНвЦКѓЕФХзЮяЯпУЛгаБфЛЏЕФВПЗжЙЙГЩвЛИіаТЕФЭМЯѓ.ЧыаДГіетИіЭМЯѓЖдгІЕФКЏЪ§
ЩЯЗНЃЌгыЦНвЦКѓЕФХзЮяЯпУЛгаБфЛЏЕФВПЗжЙЙГЩвЛИіаТЕФЭМЯѓ.ЧыаДГіетИіЭМЯѓЖдгІЕФКЏЪ§![]() yЕФНтЮіЪНЃЌВЂдкЫљИјЕФЦНУцжБНЧзјБъЯЕжажБНгЛГіМђЭМЃЌЭЌЪБаДГіИУКЏЪ§дк
yЕФНтЮіЪНЃЌВЂдкЫљИјЕФЦНУцжБНЧзјБъЯЕжажБНгЛГіМђЭМЃЌЭЌЪБаДГіИУКЏЪ§дк![]() Ём
Ём![]() ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЪБЖдгІЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшвЛДЮКЏЪ§![]() ЃЌЮЪЪЧЗёДцдке§ећЪ§
ЃЌЮЪЪЧЗёДцдке§ећЪ§![]() ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ
ЪЙЕУЃЈ2ЃЉжаКЏЪ§ЕФКЏЪ§жЕ![]() ЪБЃЌЖдгІЕФxЕФжЕЮЊ
ЪБЃЌЖдгІЕФxЕФжЕЮЊ![]() ЃЌШєДцдкЃЌЧѓГі
ЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
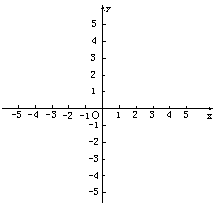
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com