
【题目】如图,将一幅直角三角板叠放在一起,使直角顶点重合于点O. 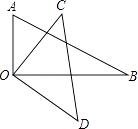
(1)若∠AOC=35°,求∠AOD的度数;
(2)问:∠AOC=∠BOD吗?说明理由;
(3)写出∠AOD与∠BOC所满足的数量关系,并说明理由.
【答案】
(1)解:∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠AOC+∠COD=35°+90°=125°
(2)解:∠AOC=∠BOD,
理由是:∵∠AOB=∠COD=90°,
∴∠AOB﹣∠COB=∠COD﹣∠COB,
∴∠AOC=∠BOD
(3)解:∠AOD+∠BOC=180°,
理由是:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠COD+∠BOC
=∠COD+∠AOB
=90°+90°
=180°
【解析】(1)把已知角的度数代入∠AOD=∠AOC+∠COD,求出即可;(2)已知∠AOB=∠COD=90°,都减去∠COB即可;(3)根据∠AOB=∠COD=90°即可求出答案.
【考点精析】通过灵活运用余角和补角的特征,掌握互余、互补是指两个角的数量关系,与两个角的位置无关即可以解答此题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
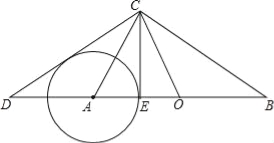
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从数学对称的角度看,下面的几组大写英文字母:①ANEC;②KBSM;③XIHO;④ZDWH中,不同于其他几组的是________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用36000元购进甲、乙两种商品,销售完后共获利6000元,其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商店购进甲、乙两种商品各多少件.
(2)商店第二次以原进价购进甲、乙两种商品.购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折降价销售。若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com