
����Ŀ����ƽ��ֱ������ϵxOy�У���֪�����ߵĶ�������Ϊ��2��0�����Ҿ����㣨4��1������ͼ��ֱ��y=![]() x�������߽���A��B���㣬ֱ��lΪy=��1��
x�������߽���A��B���㣬ֱ��lΪy=��1��
��1���������ߵĽ���ʽ��
��2����l���Ƿ����һ��P��ʹPA+PBȡ����Сֵ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3��֪F��x0��y0��Ϊƽ����һ���㣬M��m��n��Ϊ��������һ���㣬�ҵ�M��ֱ��l�ľ������M����F�ľ���������ȣ���F�����꣮

���𰸡���1�������ߵĽ���ʽΪy=![]() x2��x+1����2����P������Ϊ��
x2��x+1����2����P��������![]() ����1������3������F��������2��1����
����1������3������F��������2��1����
����������1���������ߵĶ�������Ϊ��2��0�������������ߵĽ���ʽΪy=a��x-2��2���������߹��㣨4��1�������ô���ϵ����������������ߵĽ���ʽ��
��2������ֱ��AB�������߽���ʽ�ɷ����飬ͨ���ⷽ����������A��B�����꣬����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ�����ݵ�B������ɵó���B������꣬���ݵ�A��B����������ô���ϵ���������ֱ��AB��Ľ���ʽ��������һ�κ���ͼ���ϵ�������������������P�����ꣻ
��3���ɵ�M��ֱ��l�ľ������M����F�ľ���������Ƚ�϶��κ���ͼ���ϵ���������������ɵó���1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
��1���������ߵĶ�������Ϊ��2��0����
�������ߵĽ���ʽΪy=a��x-2��2��
�߸������߾����㣨4��1����
��1=4a����ã�a=![]() ��
��
�������ߵĽ���ʽΪy=![]() ��x-2��2=
��x-2��2=![]() x2-x+1��
x2-x+1��
��2������ֱ��AB�������߽���ʽ�ɷ����飬�ã�
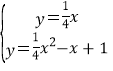 ����ã�
����ã�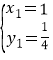 ��
��![]() ��
��
���A��������1��![]() ������B��������4��1����
������B��������4��1����
����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ����ͼ1��ʾ����
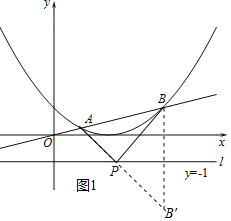
�ߵ�B��4��1����ֱ��lΪy=-1��
���B���������4��-3����
��ֱ��AB��Ľ���ʽΪy=kx+b��k��0����
��A��1��![]() ����B�䣨4��-3������y=kx+b���ã�
����B�䣨4��-3������y=kx+b���ã�
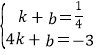 ����ã�
����ã�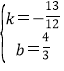 ��
��
��ֱ��AB��Ľ���ʽΪy=-![]() x+
x+![]() ��
��
��y=-1ʱ����-![]() x+
x+![]() =-1��
=-1��
��ã�x=![]() ��
��
���P��������![]() ��-1����
��-1����
��3���ߵ�M��ֱ��l�ľ������M����F�ľ���������ȣ�
�ࣨm-x0��2+��n-y0��2=��n+1��2��
��m2-2x0m+x02-2y0n+y02=2n+1��
��M��m��n��Ϊ��������һ���㣬
��n=![]() m2-m+1��
m2-m+1��
��m2-2x0m+x02-2y0��![]() m2-m+1��+y02=2��
m2-m+1��+y02=2��![]() m2-m+1��+1��
m2-m+1��+1��
�������1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
��mΪ����ֵ��
��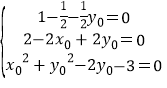 ��
��
��![]() ��
��
�ඨ��F������Ϊ��2��1����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ,
,![]() =2
=2![]() ,
,![]() Ϊ
Ϊ![]() ���е㣬������̶ȵ�ֱ���ֱ�����Ҫ��ͼ(������ͼ�ۼ�)
���е㣬������̶ȵ�ֱ���ֱ�����Ҫ��ͼ(������ͼ�ۼ�)
��1����ͼ1�У�������ABD��BD���ϵ����ߣ�
��2����ͼ2�У���BA=BD, ������ABD��AD���ϵĸ� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�![]() ��
��![]() ��E��AB��һ�㣬����CE���ֽ�
��E��AB��һ�㣬����CE���ֽ�![]() ���Ϸ����ۣ��ۺ�ΪCE��ʹ��B���ڵ�P����
���Ϸ����ۣ��ۺ�ΪCE��ʹ��B���ڵ�P����

��1������P����CD��ʱ��![]() _____������P�ھ����ڲ�ʱ��BE��ȡֵ��Χ��_____��
_____������P�ھ����ڲ�ʱ��BE��ȡֵ��Χ��_____��
��2������E���A�غ�ʱ���ٻ������ۺ��ͼ�Σ��߹���ͼ��������ͼ�ۼ�����������PD����֤��![]() ��
��

��3����ͼ���������ھ���ABCD�ĶԽ�����ʱ����BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC��AB��AC�������Ϊ��ֵ����P��ֱ��BC�ϣ���P��ֱ��AC�ľ���ΪPF����PF��3��C��AB�ľ���CH��7ʱ��P��AB�ľ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã����С�C��90�㣮
��1���������֣���ͼ2������B����DEC��30�㣬�̶���ABC��ʹ��DEC�Ƶ�C��ת������Dǡ������AB��ʱ����գ�
���߶�DE��AC��λ�ù�ϵ���� ����
�����BDC�����ΪS1����AEC�����ΪS2��S1��S2��������ϵ���� ����
��2��������֤
����DEC�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����S1��S2��������ϵ��Ȼ����������֤��С���IJ��룻
��3����չ̽��
��ͼ4����BC��3��AC��2������DEC�Ƶ�C��ת�Ĺ����У��ı���ABDE������Ƿ�������ֵ�������ڣ�����������������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������̶ӷֱ�ͬʱ�������κ��������ں����ij���y(m)���ھ�ʱ��x(h)֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ�����������:

(1)�Ҷӿ��ڵ�30mʱ������_____ h. ����6hʱ�ӱ��ҶӶ�����____ m;
(2)�������:
�ټ���![]() ��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
���Ҷ���![]() ��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
(3)��x Ϊ��ֵʱ���ס� �������� ʩ�����������ں����ij������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=30������B=62����CEƽ����ACB��CD��AB��D��DF��CE��F������CDF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����1000��ѧ����Ϊ���˽����ǵ�����������������˲���ѧ������������������������������Ƴ�ֱ��ͼ������ͼ.

��1����ι������˶�����ѧ��������ͼ�е�![]() ��
��![]() ֵ�ֱ��Ƕ��٣�
ֵ�ֱ��Ƕ��٣�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���ڹ��߽ϰ��Ļ�����ѧϰ��ѧ��ռ��Ӧ������ѧ���ı������±���
���� |
| 0.35��0.65 | 0.65��0.95 | 0.95��1.25 | 1.25��l.55 |
���� |
|
|
|
|
|
���ݵ��������Ƹ�У�ж���ѧ���ڹ��߽ϰ��Ļ�����ѧϰ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ������ԭ�㣬
������ԭ�㣬![]() ��
��![]() ��
��![]() ��Ϊ�ȱ������Σ�
��Ϊ�ȱ������Σ�![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ����
����![]() ����
����![]() ��
��![]() �ڲ�����
�ڲ�����![]() ��
��![]() ���ⲿ��
���ⲿ��![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() .
.

��1�����![]() �����ꣻ
�����ꣻ
��2���ж�![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��3��ֱ��д��![]() ���ܳ�.
���ܳ�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com