
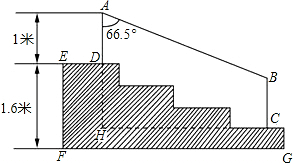
 某商场门前的台阶截面如图中阴影部分所示,已知台阶有四级小台阶且每一级小台阶高度相等,台阶高度EF为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC(杆子的低端分别为D,C),且∠DAB=66.5°(cos66.5°≈0.4).
某商场门前的台阶截面如图中阴影部分所示,已知台阶有四级小台阶且每一级小台阶高度相等,台阶高度EF为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC(杆子的低端分别为D,C),且∠DAB=66.5°(cos66.5°≈0.4).分析 (1)根据题意,可以得到DH是EF 的四分之三,从而可以求得DH的长度;
(2)根据题意,连接DC,然后根据平行四边形的性质和锐角三角函数可以求得AB的长度,从而可以求得所用不锈钢材料的总长度.
解答 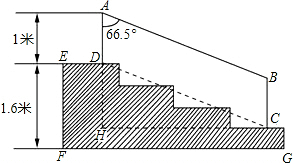 解:(1)由题意可得,
解:(1)由题意可得,
DH=1.6×$\frac{3}{4}$=1.2(米),
即点D与点C的高度差DH是1.2米;
(2)连接CD,如右图所示,
∵AD∥BC,AD=BC,∠DAB=66.5°,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠HDC=∠DAB=66.5°,
∵在Rt△HDC中,cos∠HDC=$\frac{DH}{CD}$,AD=BC=1米,
∴CD=$\frac{DH}{cos66.5°}≈\frac{1.2}{0.4}=3$(米),
∴AD+AB+BC=1+3+1=5(米),
即所用不锈钢材料的总长度是5米.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
 如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.
如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com