练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

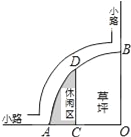
    【题目】如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是6米，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区（阴影部分）的面积是（　　）

    A. （10π﹣）米2 B. （π﹣）米2 C. （6π﹣）米2 D. （6π﹣）米2

    【答案】C

    【解析】试题分析：先根据半径OA长是6米，C是OA的中点可知OC=OA=3，再在Rt△OCD中，利用勾股定理求出CD的长，根据锐角三角函数的定义求出∠DOC的度数，由S阴影=S扇形AOD-S△DOC即可得出结论．

    试题解析：连接OD，

    ∵弧AB的半径OA长是6米，C是OA的中点，

    ∴OC=OA=×6=3米，

    ∵∠AOB=90°，CD∥OB，

    ∴CD⊥OA，

    在Rt△OCD中，

    ∵OD=6，OC=3，

    ∴CD=米，

    ∵sin∠DOC=，

    ∴∠DOC=60°，

    ∴S阴影=S扇形AOD-S△DOC==（6π-）米2

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；

    ③3a+c＞0；④当y＞0时，x的取值范围是﹣1≤x＜3；

    ⑤当x＜0时，y随x增大而增大．

    其中结论正确的个数是（　　）

    A. 4个 B. 3个 C. 2个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，动点P在平面直角坐标系中按图中的箭头所示方向运动，第一次从原点运动到点（2，2）第2次运动到点A（4，0），第3次接着运动到点（6，1）……按这样的运动规律，经过第2018次运动后动点P的坐标是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E．

    （1）求证：四边形CODE是矩形．

    （2）若AB=5，AC=6，求四边形CODE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50分才乘上缆车，缆车的平均速度为180米/分，设小亮出发x分后行走的路程为y米．图中的折线表示小亮在整个行走过程中y随x的变化关系.

    （1)小亮行走的总路程是_________米，他途中休息了___________分；

    （2）分别求出小亮在休息前和休息后所走的路程段上的步行速度；

    （3）当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）阅读下文，寻找规律：

    已知 x≠1 时，（1－x)（1＋x)＝1－x，

    (1－x)(1＋x＋x)＝1－x，

    (1－x)(1＋x＋x＋x)＝1－x.…

    观察上式，并猜想：

    (1－x)(1＋x＋x＋ x＋x)＝ ____________. (1－x)(1＋x＋x＋…＋x)＝ ____________.

    （2） 通过以上规律，请你进行下面的探素：

    ①(a－b)(a＋b)＝ ____________.

    ②(a－b)(a＋ab＋b)＝ ____________.

    ③(a－b)(a＋a＋ab＋b )＝ ____________.

    （3） 根据你的猜想，计算：

    1＋2＋2＋…＋2＋2＋2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为迎接五一节，重百超市计划销售枇杷和樱桃两种水果共5000千克，若枇杷的数量是樱桃的2倍少1000千克．

    （1）超市计划销售枇杷多少千克？

    （2）若超市从某一果园直接进货，果园共30名员工负责采摘这两种水果，每人每天能够采摘30千克枇杷或10千克樱桃，应分别安排多少人采摘枇杷和樱桃，才能确保采摘两种水果所用的时间相同？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高0.5元其销售量就减少10件，

    （1）问应将每件售价定为多少元时，才能使每天利润为640元且成本最少？

    （2）问应将每件售价定为多少元时，才能使每天利润最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

    (1)求证:AE=2CE;

    (2)连接CD,请判断△BCD的形状,并说明理由.

    查看答案和解析>>

    同步练习册答案