
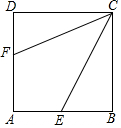
 如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.
如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$. 分析 首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易得△GCF≌△ECF,利用勾股定理可得AE=3,设AF=x,利用GF=EF,解得x,利用勾股定理可得CF.
解答 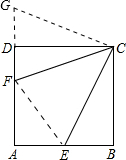 解:如图,延长FD到G,使DG=BE;
解:如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,$\left\{\begin{array}{l}{CB=CD}\\{∠CBE=∠CDG}\\{BE=DG}\end{array}\right.$,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,
$\left\{\begin{array}{l}{GC=EC}\\{∠GCF=∠ECF}\\{CF=CF}\end{array}\right.$,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵CE=3$\sqrt{5}$,CB=6,
∴BE=$\sqrt{C{E}^{2}-C{B}^{2}}$=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}$=3,
∴AE=3,
设AF=x,则DF=6-x,GF=3+(6-x)=9-x,
∴EF=$\sqrt{A{E}^{2}+{x}^{2}}$=$\sqrt{9+{x}^{2}}$,
∴(9-x)2=9+x2,
∴x=4,
即AF=4,
∴GF=5,
∴DF=2,
∴CF=$\sqrt{C{D}^{2}+D{F}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
故答案为:2$\sqrt{10}$.
点评 本题主要考查了全等三角形的判定及性质,勾股定理等,构建全等三角形,利用方程思想是解答此题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:选择题
| 引体向上的个数 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 1 | 4 | 5 |
| A. | 10和9 | B. | 9和10 | C. | 10和9.5 | D. | 9.5和10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
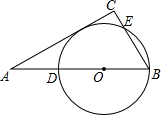 如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.
如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
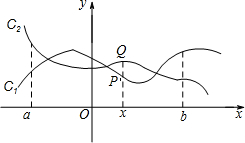 如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.
如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
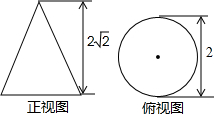 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
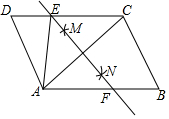 如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.
如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com