
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.

【答案】(1)![]() ;
;
(2)∠AOP=∠AOH+∠POH=45o+45o=90o;
(3)存在,直线AC解析式为![]()
【解析】试题分析:(1)根据已知点的坐标利用待定系数法确定二次函数的解析式即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,
试题解析:(1)由题意,得
 ,解得
,解得![]() .
.
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则![]()
解得 ,
,
∴直线AC解析式为y=![]() x+3
x+3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a=______________;
+b+3=0,其中a、b为有理数,那么a=______________;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两点的坐标分别为(1,0)、(0,2),若将线段AB平移至A1B1 , 点A1、B1的坐标分别为(2,a),(b,3),则a+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S2+S3+S4= 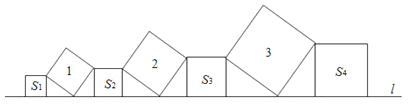
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com