
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.

【答案】(1)证明见解析(2)6
【解析】分析:(1)连接OC,根据题意可证得∠CAD+∠DCA=90°,再根据角平分线的性质,得∠DCO=90°,则CD为 O的切线;
(2)过O作OF⊥AB,则∠OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形,设AD=x,在Rt△AOF中,由勾股定理得(5-x)![]() +(6-x)
+(6-x)![]() =25,从而求得x的值,由勾股定理得出AB的长.
=25,从而求得x的值,由勾股定理得出AB的长.
本题解析

(1)证明:连接OC,∵OA=OC,∴∠OCA=∠OAC,∵AC平分∠PAE,
∴∠DAC=∠CAO,∴∠DAC=∠OCA,∴PB∥OC,∵CD⊥PA,
∴CD⊥OC,CO为O半径,∴CD为O的切线;
(2)过O作OF⊥AB,垂足为F,∴∠OCD=∠CDA=∠OFD=90,∴四边形DCOF为矩形,∴OC=FD,OF=CD.∵DC+DA=6,设AD=x,则OF=CD=6x,∵O的直径为10,∴DF=OC=5,∴AF=5x,
在Rt△AOF中,由勾股定理得AF![]() +OF
+OF![]() =OA
=OA![]() .
.
即(5x) ![]() +(6x)
+(6x) ![]() =25,化简得x
=25,化简得x![]() 11x+18=0,
11x+18=0,
解得![]() .
.
∵CD=6x大于0,故x=9舍去,∴x=2,从而AD=2,AF=52=3,
∵OF⊥AB,由垂径定理知,F为AB的中点,∴AB=2AF=6.


科目:初中数学 来源: 题型:
【题目】菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:
(1)求点D的坐标;
(2)若反比例函数y=![]() (k≠0)的图象经过点H,则k= ;
(k≠0)的图象经过点H,则k= ;
(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励该校在南山区第二届学生技能大赛中表现突出的20名同学,派李老师为这些同学购买奖品,要求每人一件,李老师到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求笔记本和钢笔的单价分别为多少元?
(2)售货员提示,购买笔记本没有优惠:买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>10)支钢笔,所需费用为y元,请你求出y与x之间的函数关系式;
(3)在(2)的条件下,如果买同一种奖品,请你帮忙计算说明,买哪种奖品费用更低.
查看答案和解析>>
科目:初中数学 来源: 题型:
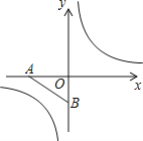
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(-![]() ,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=
,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)若点D在y轴上,点E在反比例函数y=![]() 的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线 x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)方程a(x﹣1)2 + b(x﹣1)+c=0的两根是x1= 0,x2= 6.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程
有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c ;
是“倍根方程”,则c ;
(2)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值;
的值;
(3)若方程![]() 是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线
是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() 的根.
的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,将线段BO绕点B顺时针旋转60°到BM,连接CM,OM.
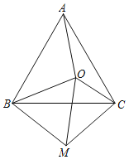
(1)求证:AO=CM;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
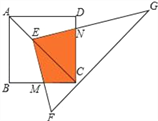
A. ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a2
a2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com