
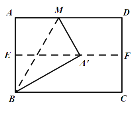
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
【答案】A
【解析】
根据折叠性质可得BE=![]() AB,A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,可得∠EA′B=30°,根据直角三角形两锐角互余可得∠EBA′=60°,进而可得∠ABM=30°,在Rt△ABM中,利用∠ABM的余弦求出BM的长即可.
AB,A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,可得∠EA′B=30°,根据直角三角形两锐角互余可得∠EBA′=60°,进而可得∠ABM=30°,在Rt△ABM中,利用∠ABM的余弦求出BM的长即可.
∵对折矩形纸片ABCD,使AD与BC重合,AB=4,
∴BE=![]() AB=2,∠BEF=90°,
AB=2,∠BEF=90°,
∵把纸片展平,再一次折叠纸片,使点A落在EF上的点A’处,并使折痕经过点B,
∴A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,
∴∠EA′B=30°,
∴∠EBA′=60°,
∴∠ABM=30°,
∴在Rt△ABM中,AB=BM![]() cos∠ABM,即4=BM
cos∠ABM,即4=BM![]() cos30°,
cos30°,
解得:BM=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】定义:两条长度相等,且它们所在的直线互相垂直的线段,我们称其互为“等垂线段”.
知识应用:在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC, ∠ACB=∠AED=90°,连接BD,点P是线段BD的中点,连接PC,PE.
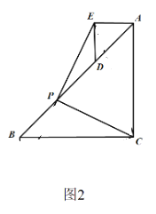
(1)如图1,当AE在线段AC上时,线段PC与线段PE是否互为“等垂线段”?请说明理由.
(2)如图2,将图1中的△ADE绕点A顺时针旋转90°,点D落在AB边上,请说明线段PC与线段PE互为“等垂线段”.
拓展延伸:(3)将图1中的△ADE绕点A顺时针旋转150°,若BC=3,DE=1,求PC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:
![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是![]() ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;
(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为![]() ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
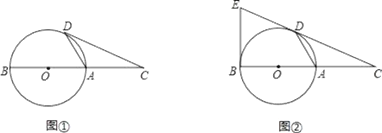
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲口罩每袋的售价比乙口罩多5元,小明从该药店购买了3袋甲口罩和2袋乙口罩共花费115元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元?
(2)根据消费者需求,药店决定用不超过8000元购进甲、乙两种口罩共400袋.已知甲口罩每袋的进价为22.2元,乙口罩每袋的进价为17.8元,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
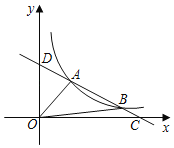
【题目】如图,点A(m,3)、B(6,n)在双曲线y=![]() (x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(1)求双曲线y=![]() 的函数表达式;
的函数表达式;
(2)求△COD的周长;
(3)直接写出不等式![]() -ax>b的解集.
-ax>b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
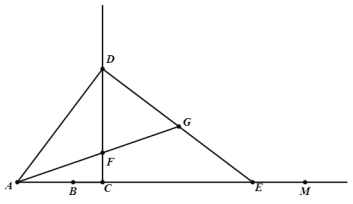
【题目】如图,射线AM上有一点B,AB=6.点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=![]() AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
(1) 当C在B点右侧时,求AD、DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形.
(3)若将△DFG沿FG翻折,恰使点D对应点![]() 落在射线AM上,连接
落在射线AM上,连接![]() ,
,![]() .此时x的值为 (直接写出答案)
.此时x的值为 (直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com