
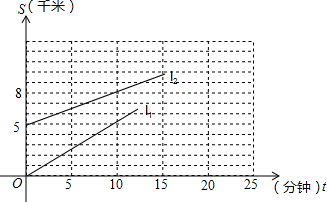
 某出租车司机送一客人到长途汽车站后不久,发现客人的皮包还留在车上.因交谈中知道客人要乘车到昆明.于是出租车司机马上驱车追赶已经出发的客车.下图中l1,l2两条线分别表示两车相对车站的距离s与追赶的时间t之间的关系.
某出租车司机送一客人到长途汽车站后不久,发现客人的皮包还留在车上.因交谈中知道客人要乘车到昆明.于是出租车司机马上驱车追赶已经出发的客车.下图中l1,l2两条线分别表示两车相对车站的距离s与追赶的时间t之间的关系. ,
, t;
t;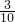 ,
,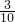 t+5,
t+5, t=
t=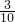 t+5,
t+5,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
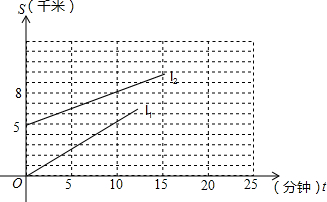 某出租车司机送一客人到长途汽车站后不久,发现客人的皮包还留在车上.因交谈中知道客人要乘车到昆明.于是出租车司机马上驱车追赶已经出发的客车.下图中l1,l2两条线分别表示两车相对车站的距离s与追赶的时间t之间的关系.
某出租车司机送一客人到长途汽车站后不久,发现客人的皮包还留在车上.因交谈中知道客人要乘车到昆明.于是出租车司机马上驱车追赶已经出发的客车.下图中l1,l2两条线分别表示两车相对车站的距离s与追赶的时间t之间的关系.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
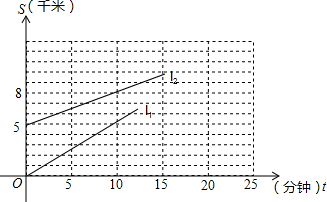
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com