
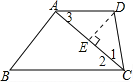
【题目】如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )

A.9![]() B.12C.8D.8
B.12C.8D.8![]()
【答案】A
【解析】
根据角平分线的定义可得∠1=∠2,根据两直线平行,内错角相等可得∠2=∠3,然后得到∠1=∠3,再根据等角对等边可得CD=AD=4,过点D作DE⊥AC于E,根据等腰三角形三线合一的性质可得AE=![]() AC,根据两组角对应相等的两个三角形相似求出△ABC∽△EDC,再根据相似三角形对应边成比例求出BC,然后利用勾股定理求出AC,从而得出DE的长,最后根据四边形的面积=S△ABC+S△ADC,即可得出答案.
AC,根据两组角对应相等的两个三角形相似求出△ABC∽△EDC,再根据相似三角形对应边成比例求出BC,然后利用勾股定理求出AC,从而得出DE的长,最后根据四边形的面积=S△ABC+S△ADC,即可得出答案.
∵CA是∠BCD的平分线,
∴∠1=∠2,
∵AD∥BC,
∴∠2=∠3,
∴∠1=∠3,
∵AD=4,
∴CD=AD=4,
过点D作DE⊥AC于E,则AE=CE=![]() AC,
AC,
∵∠1=∠2,∠BAC=∠DEC,
∴△ABC∽△EDC,
∴![]() ,
,
即 ![]() ,
,
∴BC=8,
在Rt△ABC中,AC=![]() ,
,
∴四边形的面积为:![]() ACDE=
ACDE=![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°, BC=10,AC=6,过点A作BC的平行线l,P为直线l上的动点,且△BCP是等腰三角形,则AP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个大正方形和四个全等的小正方形按图①、②两种方式摆放,设小正方形的边长为x,请仔细观察图形回答下列问题.
(1)用含a、b的代数式表示x,则x= .
(2)用含a、b的代数式表示大正方形的边长 .(请将结果化为最简)
(3)利用前两问的结论求出图②的大正方形中未被小正方形覆盖部分的面积.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En,则O2016E2016=_____AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,4),与x轴的一个交点是B(3,0),下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=4有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣2.0);⑤x(ax+b)≤a+b,其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com