
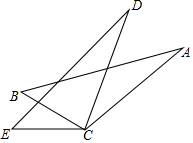
 如图,AC=DC,BC=EC,请你添加一个适当的条件:AB=DE,使得△ABC≌△DEC.
如图,AC=DC,BC=EC,请你添加一个适当的条件:AB=DE,使得△ABC≌△DEC. 科目:初中数学 来源: 题型:解答题
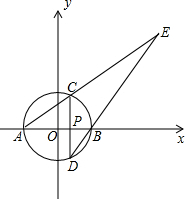 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
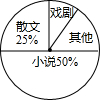 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3<x≤2 | B. | -3≤x<2 | C. | x≥2 | D. | x<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
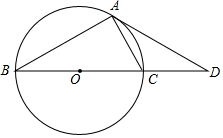 如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com