
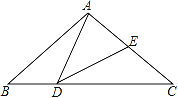
【题目】如图,△ABC中,AB=AC=2,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC= °;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由
【答案】(1)20;(2)当![]() 时,
时,![]() ,理由详见解析;(3)当
,理由详见解析;(3)当![]() 或60°时,
或60°时,![]() 为等腰三角形
为等腰三角形
【解析】
(1)利用三角形的外角的性质得出答案即可;
(2)利用∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC得出∠BAD=∠EDC,进而求出△ABD≌△DCE;
(3)根据等腰三角形的判定以及分类讨论得出即可.
解:(1)∵∠BAD=20°,∠B=40°,
∴∠ADC=60°,
∵∠ADE=40°,
∴∠EDC=60°-40°=20°,
故答案为:20;
(2)当![]() 时,
时,![]() ,
,
理由:∵![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
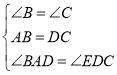
∴![]() ;
;
![]() .
.
(3)能,当∠BAD=30°或60°时,△ADE能成为等腰三角形.
理由:①当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,这时
,这时![]() 为等腰三角形,
为等腰三角形,
②当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴![]() ,这时
,这时![]() 为等腰三角形.
为等腰三角形.
综上所述,当∠BAD=30°或60°时,△ADE能成为等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
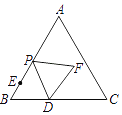
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
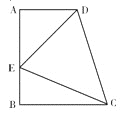
【题目】如图,在梯形ABCD中,∠A=∠B=90°,AB=![]() ,点E在AB上,∠AED=45°,DE=6,CE=7.
,点E在AB上,∠AED=45°,DE=6,CE=7.
(1)求AE的长;
(2)求sin∠BCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
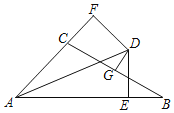
【题目】如图,∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE的长( )
A.3B.2C.5D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球.学生可根据自己的爱好选择一项,李老师对八年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
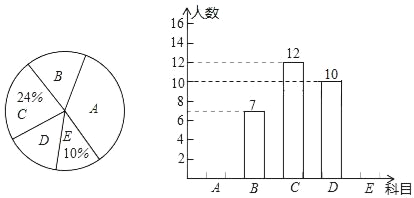
A. 选科目E的有5人
B. 选科目A的扇形圆心角是120°
C. 选科目D的人数占体育社团人数的![]()
D. 据此估计全校1000名八年级同学,选择科目B的有140人
查看答案和解析>>
科目:初中数学 来源: 题型:
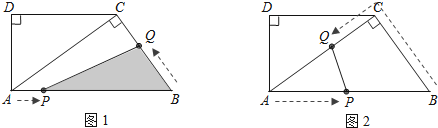
【题目】如图1,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,BC=6cm. 点P以1cm/s的速度从点A出发,沿AB方向向点B运动,同时点Q以2cm/s的速度从点B出发,沿B→C→A方向向点A运动,当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)① 求证:△ACD∽△BAC;② 求DC的长;
(2)当点Q在边BC上运动,求t为何值时,△PBQ的面积为![]() cm2;
cm2;
(3)如图2,当点Q在边CA上运动,求t为何值时,PQ∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书, 于是又折回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
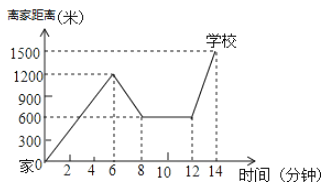
(1)小明家到学校的距离是__ _米;
(2)小明在书店停留了 分钟;
(3)本次上学途中,小明一共骑行了 米;
(4)我们认为骑车的速度超过了![]() 米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由,
米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com