
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.

【答案】(1)证明见解析;(2)3;(3)![]()
【解析】
(1)连接OC,如图1,先证明∠1=∠3得到OC∥AD,再利用平行线的性质得OC⊥CD,然后根据切线的判定定理得到结论;
(2)连接BE交OC于H,如图1,利用圆周角定理得∠AEB=90°,易得四边形CDEH为矩形,则CD=EH=3![]() ,CH=ED,利用垂径定理得BH=3
,CH=ED,利用垂径定理得BH=3![]() ,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
(3)连接OC,如图2,设⊙O的半径为r,利用角平分线的性质得CD=CF,则根据勾股定理得AD=AF,于是可计算出OF=1.5,再证明△ACF∽△ABC,利用相似比得到![]() ,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=
,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=![]() ,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
(1)连接OC,如图1,
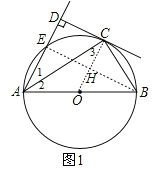
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O切线;
(2)连接BE交OC于H,如图1,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵OC∥AD,
∴∠OHB=90°,
∴EH=BH,四边形CDEH为矩形,
∴CD=EH=3![]() ,CH=ED,
,CH=ED,
∴BH=3![]() ,
,
在Rt△OBH中,OH=![]() =3,
=3,
∴CH=6-3=3,
∴DE=3;
(3)连接OC,如图2,设⊙O的半径为r,
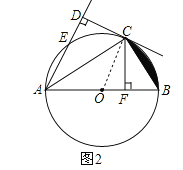
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CD=CF,
∴AD=AF=AO+OF,
∵AD-OA=1.5,
∴AO+OF-OA=1.5,即OF=1.5,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴![]() ,即
,即![]() ,
,
解得r=-![]() (舍去)或r=3,
(舍去)或r=3,
在Rt△OCF中,cos∠COF=![]() ,
,
∴∠COF=60°,
∴CF=![]() OF=
OF=![]() ,
,
∴图中阴影部分面积=S扇形BOC-S△OCB=![]() -
-![]() ×3×
×3×![]() =
=![]() π-
π-![]() .
.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>﹣1;④关于x的方程ax2+bx+c=0有一个根为﹣![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
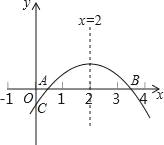
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
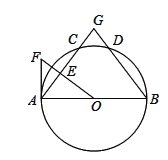
【题目】如图,AB是⊙O的直径,C、D为⊙O上两点,且![]() ,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
,过点O作OE⊥AC于点E,⊙O的切线AF交OE的延长线于点F,弦AC、BD的延长线交于点G.
(1)求证:∠F=∠B;
(2)若AB=10,BG=13,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
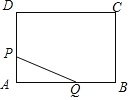
A. 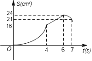 B.
B. 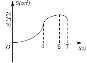 C.
C. 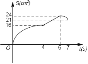 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生“平均每天体育锻炼时间”的情况,某地区教育部门随机调查了若干名中学生,根据调查结果制作统计图①和图②,请根据相关信息,解答下列问题:
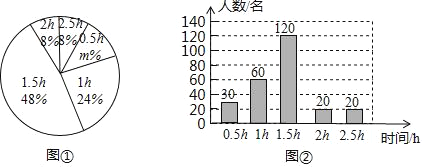
(1)本次接受随机抽样调查的中学生人数为_______,图①中m的值是_____ ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是小慧在“天猫双11”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,己知两支脚![]() 分米,
分米,![]() 分米,
分米,![]() 为
为![]() 上固定连接点,靠背
上固定连接点,靠背![]() 分米.档位为Ⅰ档时,
分米.档位为Ⅰ档时,![]() ,档位为Ⅱ档时,
,档位为Ⅱ档时,![]() .当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端
.当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端![]() 向后靠的水平距离(即
向后靠的水平距离(即![]() )为______分米.
)为______分米.
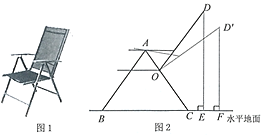
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com