
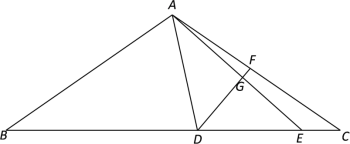
【题目】已知:如图,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2 =BE · DC ,DE:EC=3:1 ,F是边AC上的一点,DF与AE交于点G.
(1)找出图中与△ACD相似的三角形,并说明理由;
(2)当DF平分∠ADC时,求DG:DF的值;
(3)如图,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.
【答案】(1)△ABE、△ADC,理由见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据相似三角形的判定方法,即可找出与△ACD相似的三角形;
(2)由相似三角形的性质,得![]() ,由DE=3CE,先求出AD的长度,然后计算得到
,由DE=3CE,先求出AD的长度,然后计算得到![]() ;
;
(3)由等腰直角三角形的性质,得到∠DAG=∠ADF=45°,然后证明△ADE∽△DFA,得到![]() ,求出DF的长度,即可得到
,求出DF的长度,即可得到![]() .
.
解:(1)与△ACD相似的三角形有:△ABE、△ADC,理由如下:
∵AB2 =BE · DC ,
∴![]() .
.
∵AB=AC,
∴∠B=∠C,![]() ,
,
∴△ABE∽△DCA.
∴∠AED=∠DAC.
∵∠AED=∠C+∠EAC,∠DAC=∠DAE+∠EAC,
∴∠DAE=∠C.
∴△ADE∽△CDA .
(2)∵△ADE∽△CDA,DF平分∠ADC,
∴![]() ,
,
设CE=a,则DE=3CE=3a,CD=4a,
∴![]() ,解得
,解得![]() (负值已舍)
(负值已舍)
∴![]() ;
;
(3)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45° ,
∴∠DAE=∠C=45°,
∵DG⊥AE,
∴∠DAG=∠ADF=45°,
∴AG=DG=![]() ,
,
∴![]() ,
,
∵∠AED=∠DAC ,
∴△ADE∽△DFA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,将四边形
上,将四边形![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 、
、![]() 的对称点分别记为
的对称点分别记为![]() 、
、![]() .
.
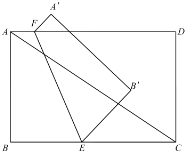
(1)当![]() 时,若点
时,若点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的长;
的长;
(2)设![]() ,若翻折后存在点
,若翻折后存在点![]() 落在线段
落在线段![]() 上,则
上,则![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
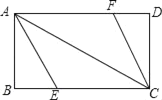
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
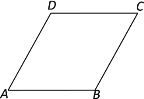
【题目】如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径![]() 米是其两腿迈出的步长之差
米是其两腿迈出的步长之差![]() 厘米
厘米![]() 的反比例函数,其图象如图所示.
的反比例函数,其图象如图所示.
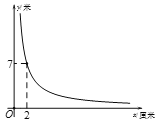
请根据图象中的信息解决下列问题:
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当某人两腿迈出的步长之差为![]() 厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于![]() 米,则其两腿迈出的步长之差最多是多少厘米?
米,则其两腿迈出的步长之差最多是多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
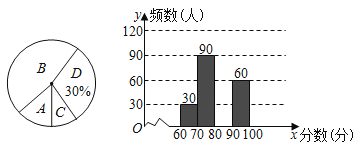
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市要选拔一名教师参加省级评优课比赛:经笔试、面试,结果小潘和小丁并列第一,评委会决定通过摸球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个蓝球,小潘先取出一个球,记住颜色后放回,然后小丁再取出一个球.若两次取出的球都是红球,则小潘胜出;若两次取出的球是一红一蓝,则小丁胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的
为直径的![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,点
,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .
.
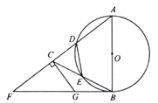
(1)试说明![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com