
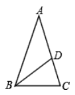
【题目】如图,在等腰三角形ABC中,AB=AC,点D为AC上一点,且AD=BD=BC,则等腰三角形ABC的顶角度数为__________________.
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°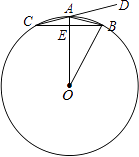
(1)求∠AOB的度数;
(2)若AE=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据如表回答下列问题:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)275.56的平方根是______ ;
(2)![]() = ______ ;
= ______ ;
(3)查看上表, <![]() < .
< .
查看答案和解析>>
科目:初中数学 来源: 题型:
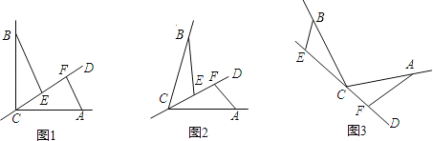
【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2 ![]() ,2
,2 ![]() )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
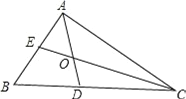
【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com