
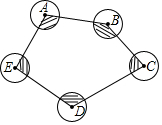
 如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.
如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2. 科目:初中数学 来源: 题型:解答题
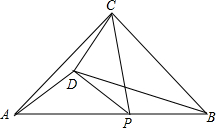 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
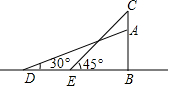 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)
如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
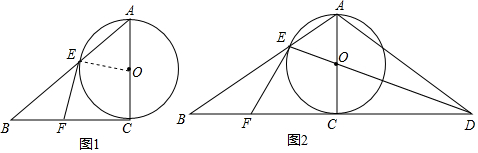
| A. | AB=$\frac{1}{2}$AC | B. | AB=BC | C. | AC=2AB | D. | AB+BC=AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com