
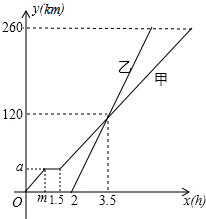
 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据“路程÷时间=速度”由函数图象就可以求出甲的速度,求出a的值和m的值解答①;根据函数图象可得乙车行驶3.5-2=1小时与甲车相遇解答②;再求出甲、乙车行驶的路程y与时间x之间的解析式解答③;由解析式之间的关系建立方程解答④.
解答 解:由题意,得
m=1.5-0.5=1.
120÷(3.5-0.5)=40(km/h),
则a=40.
∴甲车行驶40千米开始休息,
故①正确;
根据函数图象可得乙车行驶3.5-2=1.5小时与甲车相遇,故②错误;
当0≤x≤1时,设甲车y与x之间的函数关系式为y=k1x,由题意,得:
40=k1,
则y=40x
当1<x≤1.5时,
y=40;
当1.5<x≤7时,
设甲车y与x之间的函数关系式为y=k2x+b,由题意,得:
$\left\{\begin{array}{l}{40=1.5{k}_{2}+b}\\{120=3.5{k}_{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=40}\\{b=-20}\end{array}\right.$,
则y=40x-20.
设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,由题意,得:
$\left\{\begin{array}{l}{0=2{k}_{3}+{b}_{3}}\\{120=3.5{k}_{3}+{b}_{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{3}=80}\\{{b}_{3}=-160}\end{array}\right.$,
则y=80x-160.
当40x-20-50=80x-160时,
解得:x=$\frac{9}{4}$.
当40x-20+50=80x-160时,
解得:x=$\frac{19}{4}$.
$\frac{9}{4}$-2=$\frac{1}{4}$,$\frac{19}{4}$-2=$\frac{11}{4}$.
所以乙车行驶小时$\frac{1}{4}$或$\frac{11}{4}$小时,两车恰好相距50km,
故④错误;
当1.5<x≤7时,甲车y与x之间的函数关系式为y=40x-20,
当y=260时,260=40x-20,
解得:x=7,
乙车行驶的路程y与时间x之间的解析式为y=80x-160,
当y=260时,260=80x-160,
解得:x=5.25,
7-5.25=1.75(小时)
∴甲车比乙车晚1.75小时到到B地,
故③错误;
∴正确的只有①,
故选A.
点评 本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出一次函数的解析式是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-x}{y-1}=\frac{x}{y+1}$ | B. | $\frac{-x}{y-1}=\frac{-x+1}{y}$ | C. | $\frac{-x}{y-1}=\frac{x}{1-y}$ | D. | $\frac{-x}{y-1}=\frac{y-1}{-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
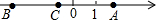 有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:
有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com