练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
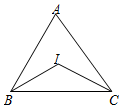
    1．如图，在△ABC中，∠A=66°，点I是内心，则∠BIC的大小为（　　）
    A．114°B．122°C．123°D．132°

    分析 根据三角形内角和定理求出∠ABC+∠ACB，根据内心的概念得到∠IBC=$\frac{1}{2}$∠ABC，∠ICB=$\frac{1}{2}$∠ACB，根据三角形内角和定理计算即可．

    解答 解：∵∠A=66°，
    ∴∠ABC+∠ACB=114°，
    ∵点I是内心，
    ∴∠IBC=$\frac{1}{2}$∠ABC，∠ICB=$\frac{1}{2}$∠ACB，
    ∴∠IBC+∠ICB=57°，
    ∴∠BIC=180°-57°=123°，
    故选：C．

    点评 本题考查的是三角形的内切圆和内心，掌握三角形的内心的概念、三角形内角和定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．已知一个多边形的每一个外角都等于72°，则这个多边形的边数是5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，∠1是五边形ABCDE的一个外角，若∠1=65°，则∠A+∠B+∠C+∠D=425°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

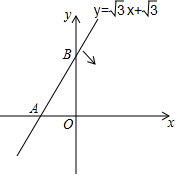    9．如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动的路径的长度为$\frac{2}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．不等式-2x＞$\frac{1}{2}$的解集是（　　）
    A．x＜-$\frac{1}{4}$B．x＜-1C．x＞-$\frac{1}{4}$D．x＞-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知一元二次方程x2-3x-2=0的两个实数根为x1，x2，则（x1-1）（x2-1）的值是-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

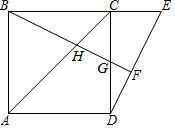    13．如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交CD于G．
    （1）求证：BG=DE；
    （2）若点G为CD的中点，求$\frac{HG}{GF}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

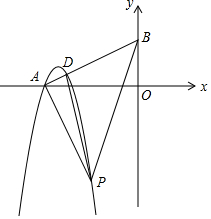    17．已知抛物线C：y=（x+2）[t（x+1）-（x+3）]，其中-7≤t≤-2，且无论t取任何符合条件的实数，点A，P都在抛物线C 上．
    （1）当t=-5 时，求抛物线C的对称轴；
    （2）当-60≤n≤-30 时，判断点（1，n）是否在抛物线C上，并说明理由；
    （3）如图，若点A在x轴上，过点A作线段AP的垂线交y轴于点B，交抛物线C于点D，当点D的纵坐标为m+$\frac{1}{2}$时，求S△PAD的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，A，B，C是⊙O上的三点，若∠BAO=65°，则∠ACB的度数是25°．

    查看答案和解析>>

    同步练习册答案